[想定している読者像]

  • MMMに興味があるマーケター / Robynの出力の見方を知りたい方
  • Robynの動かし方をある程度知っている

[読後に得られる知識]

  • RobynのOne-pagerレポートの各グラフの厳密な定義と計算方法
  • Robyn MMMモデルにおけるCPA、ROI、寄与度の数学的な定義

Robynのついての前提知識はこちらをご参照ください。

1. One-pagerレポート

Robynはモデルの要約レポートを1つの画像ファイルとして出力してくれます。これをOne-pagerレポートと呼んでいます。

具体的には以下のようなものです。

One-pagerレポート

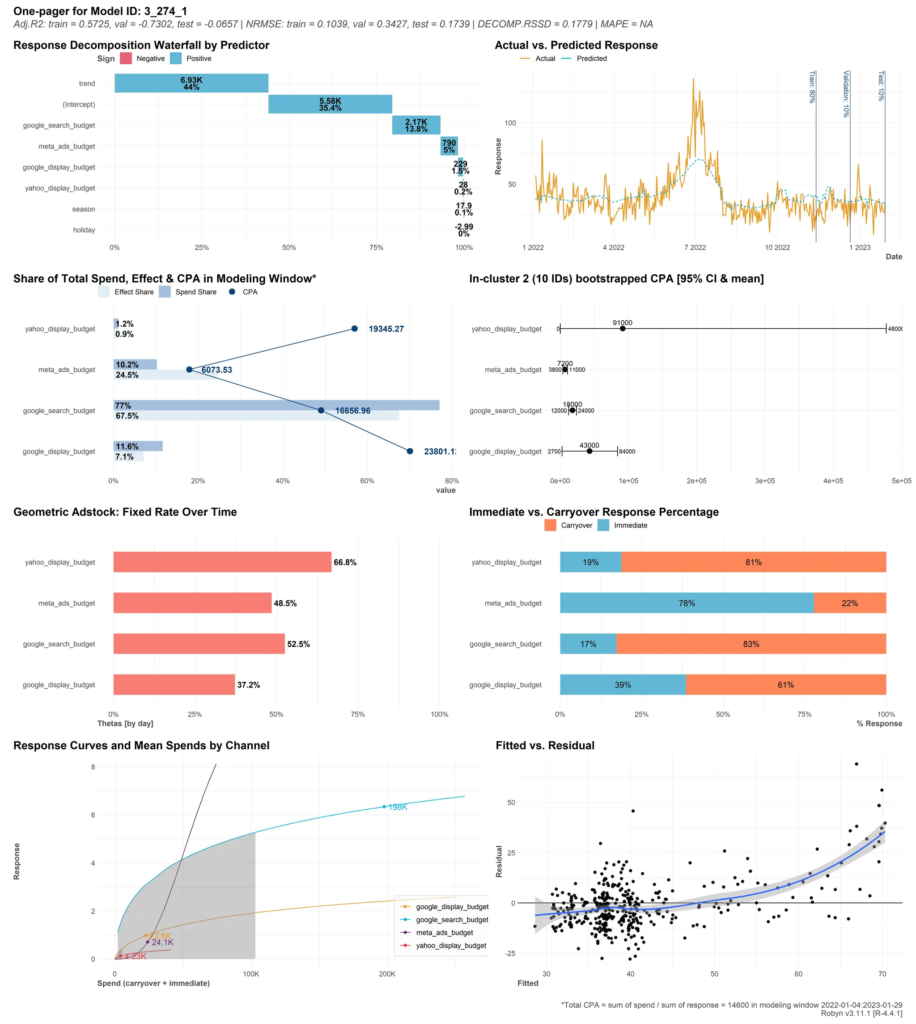
グラフで描画された指標の詳細な定義が気になります。本稿ではこれらグラフの元となる指標の定義をソースコードから読み解いていきたいと思います。

2. モデルを理解する

2.1 モデル構造

まずモデル構造を理解しましょう。Robynは回帰モデルです。その説明変数はメディア投下費用や季節性、祝日、イベント（オリンピックなど）などです。

メディアは投下日だけでなく、その翌日以降も減衰しつつ効果が続くと仮定しています。その効果を加味した変数をdecay（減衰）変数として

$$X_{m,t}^{decay}=X_{m,t} + \theta_{m}X_{m,t-1}^{decay}$$

と定義しています。mはメディアm、tは時点tを意味します。なおRobynではdecayの定義の方法を指定することができ

  • 幾何型
  • ワイブル型
    • 確率密度タイプ
    • 分布関数タイプ

を指定することが可能です。本記事では一番理解が容易な幾何型の利用を前提に説明していきます。上記式も幾何型での定義です。

広告投下を増やしていくとその効果が逓減していくと仮定し、これをモデル化するためにdecay変数を逓減関数Sに入力します。これはsaturation変数と呼ばれ、回帰モデルの入力となります。

$$X_{m,t}^{saturation}=S_{m}(X_{m,t}^{decay}).$$

逓減関数Sはヒル関数です。以下で定義されます。

$$S_{m}(X_{m,t}^{decay})=\frac{(X_{m,t}^{decay})^{\alpha_{m}}}{(X_{m,t}^{decay})^{\alpha_{m}}+inflexion_{m}^{\alpha_{m}}} \\ inflexion_{m} = (1 – \gamma_{m})×\min(X_{m,t}^{decay})+\gamma_{m} ×\max(X_{m,t}^{decay}) $$

この関数はメディアごとに異なり、その形状を決定するハイパーパラメータは\(\alpha_{m}\)と\(\gamma_{m}\)です。従ってdecay変数を定義する\(\theta_{m} \)と合わせてハイパーパラメータは(3×メディア数)だけ存在します。なおRobynのマニュアルでは定義式のinflexionの部分が\(\gamma\)になっており、注意が必要です。

季節変数は周期関数の和として定義されています。他にも任意の外部変数（競合の価格など）を入力することが可能です。これをモデル式で記述すると

$$\hat{y}_{t}=\alpha+\sum_{m \in M}\beta_{m}S_{m}(X_{m,t}^{decay})+\beta_{seasonality}Y_{seasonality,t}+\sum_{i}\beta_{i}Z_{i,t}$$

です。ここで、各々の記号は

  • \(M\): メディアの集合
  • \(Y_{seasonality,t}\): 時点tにおける季節性を表す変数（三角関数の和で表現）
  • \(Z_{i,t}\): 時点tにおけるi番目の外部変数（競合価格、イベントなど）
  • \(y_{t}\): 時点tにおける目的変数（実際の売上高やコンバージョン数）
  • \(\hat{y}_{t}\): 時点tにおける目的変数の予測値
  • \(\beta_{m}\): メディアmの効果を表す係数
  • \(\beta_{seasonality}\): 季節性の効果を表す係数
  • \(\beta_{i}\): i番目の外部変数の効果を表す係数
  • \(\alpha \): 切片（オーガニック効果）

を表しています。

逓減効果関数Sは時間t単位で計算されることに注意してください。（脚注）Robynはデータが日次なのか、週次なのか、月次なのかをデータの最初の数行の日次を見て、自動で判断しています。

2.2 モデルの学習方法

Robynはリッジ回帰モデルです、過学習を抑制するために、誤差にその係数のペナルティ項を追加したものを最小化します。誤差関数は以下で定義されます。

$$誤差関数 = (y_{t}-\hat{y}_t)^2+\lambda||\mathbf{\beta}||_{2}^2 $$

この式の各項目は以下を表しています：

  • \((y_{t}-\hat{y}_t)^2\)：実測値と予測値の二乗誤差
  • \(\lambda \)：正則化の強さを制御するハイパーパラメータ
  • \(||\mathbf{\beta}||_{2}^2\)：パラメータβのL2ノルムの二乗（各係数の二乗和）

（脚注）λを大きくすると係数が0に近づき（縮小し）、モデルが単純になります。逆にλを小さくすると係数の値が大きくなることを許容し、より複雑なモデルとなります。

ハイパーパラメータを適当に与えて、上記誤差を最小にするパラメータβを推定しています。より小さい誤差になるようなハイパーパラメータを繰り返し探索しハイパーパラメータ解とパラメータ解βを得ます。（脚注）Robynは単純な誤差の最小化ではなく、既存の予算配分との整合性のバランスを取りながら誤差を最小にするマルチ目的関数の最適化を行っています。

この学習により、得られたパラメータをまとめると

  • 各種重みパラメータ\(β_{m}、β_{seasonarity}、β_{i}\)
  • ハイパーパラメータ、\(\{θ、α、γ\}_{m}\)

です。

なお全データの何%を学習に使用するかを指定できます。train_size=0.7とすると、残りの30%をそれぞれ15%に按分したものがバリデーションデータ、テストデータとして使用されます。

Robynは内部で変数を自動的に標準化しています。

3. 基礎的な量の定義

推定されたモデルからCPAやROIなどの基礎的な量を計算します。ここで計算される量の多くがOne-pagerレポートの元データとなっています。

3.1 CPA/ROI

RobynにおいてのCPA/ROIは推定されたモデルから以下のように計算されます。

$$ CPA_{m}=\sum_{t=0}^{T}X_{m,t} / \sum_{t=0}^{T}\beta_{m}S_{m}(X_{m,t}^{decay}) \\ ROI_{m} = \frac{1}{CPA_{m}} $$

添え字mはメディアを示しています。例えばmにはTV、Googleディスプレイ広告などが入ります。

3.2 分母を全体とした場合の寄与度

モデルから得られた推定コンバージョンや売上を\(\hat{y}_{t}\)とします。寄与度は期間を通しての推定コンバージョンや売上に占める、当該変数の貢献（と推定される）コンバージョンや売上の割合で定義されます。

メディアmの貢献成果を\(\hat{y}_{m,t}\) 、季節性の貢献効果を\(\hat{y}_{seasonality,t}\)、その他の変数（のi番目の）貢献成果を\( \hat{y}_{i,t} \) は以下で計算されます。

$$ \hat{y}_{m,t} = \beta_{m}S_{m}(X_{m,t}^{decay}) \\ \hat{y}_{sesonarity,t} = \beta_{seasonality}Y_{seasonality,t} \\ \hat{y}_{i,t} = \beta_{i}Z_{i,t} .$$

寄与度はこれをコンバージョンや売上の総和で割ったものです。つまり

$$ メディアmの寄与度=\sum_{t}\hat{y}_{m,t} / \sum_{t}\hat{y}_{t} \\ 季節性の寄与度=\sum_{t}\hat{y}_{sesonarity,t}/ \sum_{t}\hat{y}_{t} \\ i番目のその他の変数の寄与度=\sum_{t}\hat{y}_{i,t} / \sum_{t}\hat{y}_{t} .$$

です。

3.3 spend shareとeffect share

メディアmのspend shareはメディアの総投下量に対しての、メディアmの投下量です。式で書くと

$$ spendshare_{m}=\sum_{t}X_{m,t} / \sum_{m}\sum_{t} X_{t,m} ,$$

です。effect shareは寄与度の分母をメディアの総貢献に置換したもので

$$effectshare_{m}= \sum_{t}\hat{y}_{m,t} / \sum_{m}\sum_{t}\hat{y}_{m,t}, $$

と記述できます。

4. OnePagerレポートのそれぞれのグラフの解説

4.1 Response Decomposition Waterfall by Predictor

まずは、寄与度をウォーターフォールグラフで表した以下の図です。

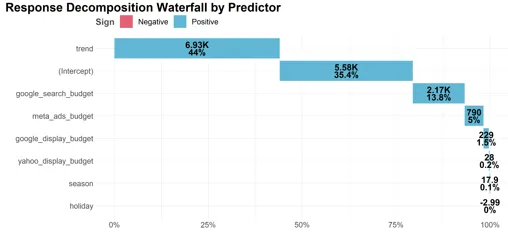
これは3.2で計算した各メディアや、季節性、その他変数の寄与度の大きい順に並べてウォーターフォールグラフにしたものです。

4.2 Actual vs predicted

実績と予測のグラフです。

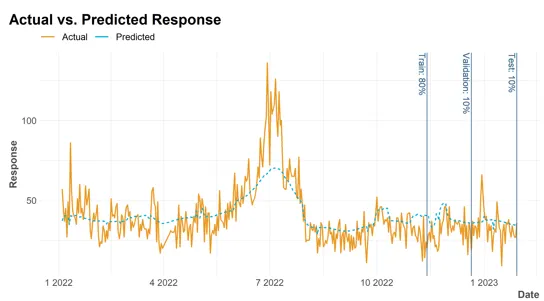
これは簡単で

実績: \(y_{t}\)
予測: \(\hat{y}_{t}\)

です。

4.3 Share of Total Spend, Effect & CPA in Modeling Window

以下の図です。

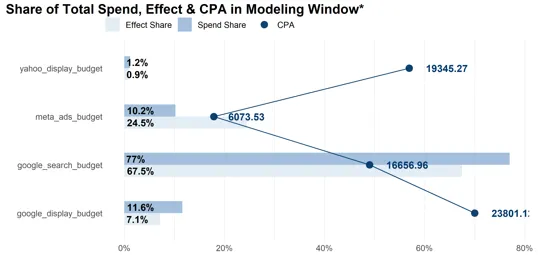
3.1で定義したCPAと、3.3で定義したspend share と effect shareを棒グラフと折れ線で表示したものです。目的変数が売上の場合、CPAではなく、ROIが表示されます。

4.4 In-cluster bootstrapped CPA (95% CI & mean)

これはやや定義がややこしく、同じクラスタ内のモデルのCPA/ROIの推定値を復元抽出し、そのバラツキをプロットしているようです。（すいませんこれはあまり自信がありません）

4.5 Geometric Adstock: Fixed Rate Over Time

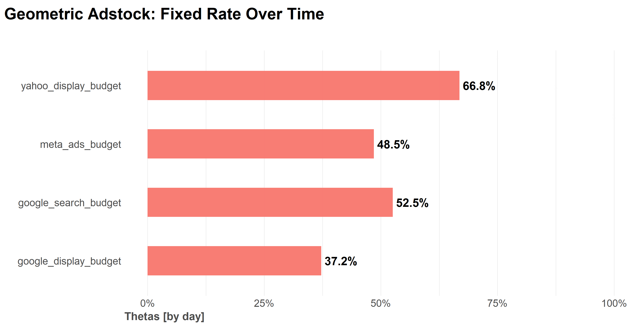
2.1の\(\theta_{m}\)そのものです。2.1でも述べましたが、アドストックオプションで「Geometric」を選択しているとこの表になります。

4.6 Immediate vs. Carryover Response Pecentage

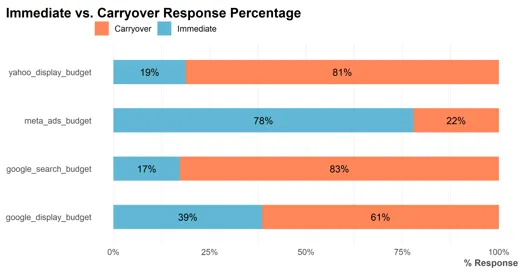
メディアの即効果と翌日への持ち越し効果の比率です。持ち越し効果比率(Carryover)の割合が大きいほど、持ち越し効果が大きいことを示しています。

計算は若干ややこしく

$$ X_{m,t}^{carryover} = X_{m,t}^{decay} – X_{m,t} \\ Immediate = \frac{\beta_{m}S_{m}(X_{m,t}^{decay}) – \beta_{m}S_{m}(X_{m,t}^{carryover})}{ \beta_{m}S_{m}(X_{m,t}^{decay})} \\ Carryover = 1-Immediate $$

と定義されます。

4.7 Response Curves and Mean Spends by Channel

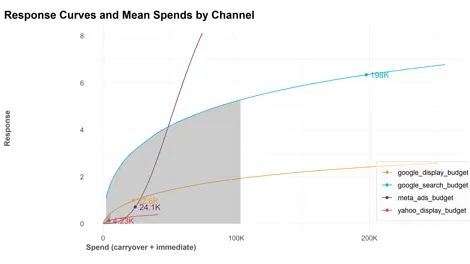
上記曲線はメディアごとに定義される \(S_{m}(X_{m,t}^{decay})\)に\(\beta_{m}\) を乗じたものです。曲線上●のマーカーは、平均値での推定値、つまり \(\beta_{m}S_{m}(mean(X_{m,t}^{decay}))\)です。影の部分は、 \(X<mean(X_{m,t}^{carryover})\)の範囲を塗りつぶしたものです。

4.8 Fitted vs. Residual

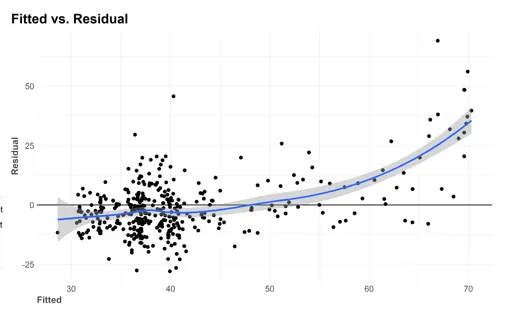
実績値と予測値の差を縦に、横軸に実績値をとった散布図です。y=0を中心に均等に残差がばらついている状態が理想です。

5. まとめ

One-pagerレポートは便利ですが、厳密な定義を理解していないと、突っ込んだ質問に対応できないかもしれません。加えて定義式を理解していれば、pythonやExcelで同じグラフを再現できます。

本稿で解説した定義をもとに、One-pagerレポートの解釈をより深めていただき、より効果的なマーケティング意思決定に活用していただければ幸いです。