[想定している読者像]
インフレによる値上げを検討している、経営者、ブランドマネージャー、経営企画の担当者様。
[コンテンツ属性]
ビジネス:★★☆☆☆
データアナリティクス:★★★★★
エンジニアリング:★☆☆☆☆
この記事ではまず近年、物価高による値上げの圧力に企業が直面していることに触れ、次に需要の価格弾力性の一般論と代表的なモデルについて解説し、最後にpythonで実際に最適価格を求める例をご紹介します。
1. はじめに
インフレが世界を席巻しています。我が国も例外ではなく、昨年から多くの品目の物価が上昇し続けています。これまで消費者価格を据え置いてきた企業も商品やサービスの値上げをする動きが出てきています。
一般的に、価格が上昇すると需要は減少すると考えられています。(ただし、生活必需品や食料品の場合はその影響が少なく、娯楽品や嗜好品の場合はその影響が大きいようです。)ではその影響の程度はどれくらいになるのでしょうか?この議論は値上げ幅を決定するための重要な問いです。例えば価格をp、需要量をQとした場合、売上はpQです。ここでpを10%値上げしたとき、Qが20%減少したとすると1.1p0.8Q=0.88p*Qとなり、売上は減少します。つまり、適切な値付けとその影響を考慮しないと思いもよらぬ損失を被ることになります。
本稿では価格弾力性と逆需要関数を用いて最適な値付けを行う方法をご紹介します。
2. 価格弾力性
2.1 定義
価格弾力性は、価格の変化が需要量に与える影響を測る指標です。需要の変化率と価格の変化率の比率として計算されます。数式的な定義は、
$$ 需要の価格弾力性 := -\frac{dQ/Q}{dp/p}$$
です。p、Qはそれぞれ現在の価格と需要量、dp,dQはその変化です。-符号があるのは、一般的に価格の変化率の正負と需要の変化率の正負が逆であるためです(つまり需要曲線は右下がり)。1需要曲線が右上がりになるギッフェン財と呼ばれるものもあるがかなり特殊
例)1杯300円の牛丼が330円に値上がりしたとき、需要単位が10→8に下がった。この場合の価格弾力性は?
$$-\frac{(8-10)/10}{330-300/300}=-\frac{0.2}{0.1}=2$$
2.2 性質
価格弾力性が1よりも大きい場合、需要は価格の変化に敏感であり、価格の上昇によって需要が減少します。逆に価格弾力性が1よりも小さい場合、需要は価格の変化に鈍感であり、価格の上昇によって需要がほとんど変化しません。前者を価格弾力的、後者を非弾力的であるといいます。下図左の例を見ると、価格が4(A)→8(B)となった場合、価格弾力性は(25-10)/10 ÷ (8-4)/4 = 1.5>1となり、弾力的です。一方、下図右の例では、(15-10)/10 ÷ (8-4)/4 = 0.5<1となり、非弾力的です。下図を逆需要曲線と呼びます2一般的に経済学のテキストでは横軸を価格、縦軸を数量(需要量)としたものを需要曲線と呼びますが、本稿では解説の利便上その逆関数を使います。
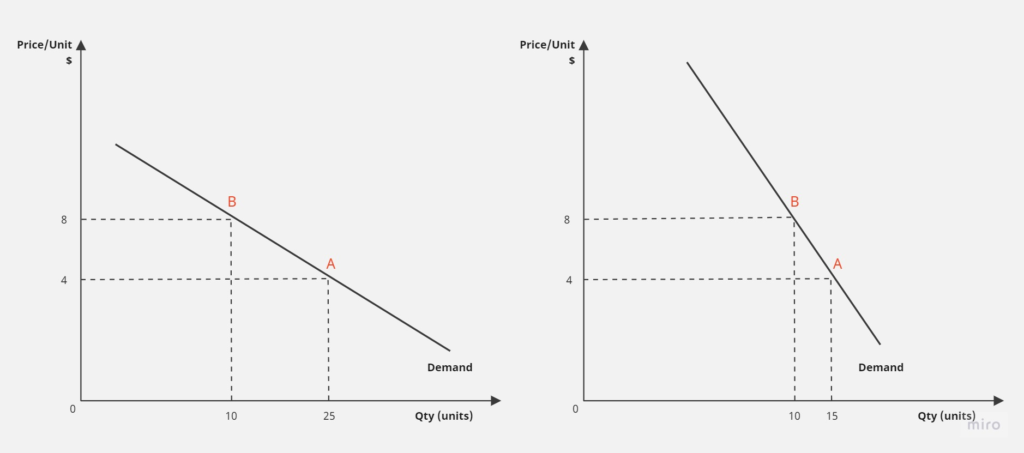
一般的には、同一の需要曲線であっても、価格の推移始点が異なれば価格弾力性は異なります。例えば相対的に価格の高い点付近での弾力性は高く、低い点付近ではその逆となります。(価格弾力性が価格に依存しない特殊なモデルもあります。2.4 参照)
2.3 逆需要曲線から弾力性を導く
逆需要曲線は価格と需要量の関係をプロットしたもので、その関係は関数fを通してQ=f(p)と書けます。この関係を用いて
$$ fをpで微分, \frac{dQ}{dp}=f'(p) \\ 価格弾力性 := -\frac{dQ/Q}{dp/p}=-\frac{p}{Q}\frac{dQ}{dp} =-\frac{p}{f(p)}f'(p) $$
とでき、価格弾力性は逆需要曲線から導くことができpの関数となります。
[例1] Q = f(p) = -p + 100の場合の価格弾力性を求める
$$-(p/f(p))f'(p) = -(p/(-p+100))*-1=(1/(-1+100/p))$$
[例2] Q = f(p) = a/p (aは定数)
$$ -(p/f(p))f'(p) = -(pp/a)-a/p^2=1 $$
つまり、逆需要曲線が微分可能な関数で定義できると需要の価格弾力性が簡単に求まるということが分かります。
2.4 特殊な場合の求め方
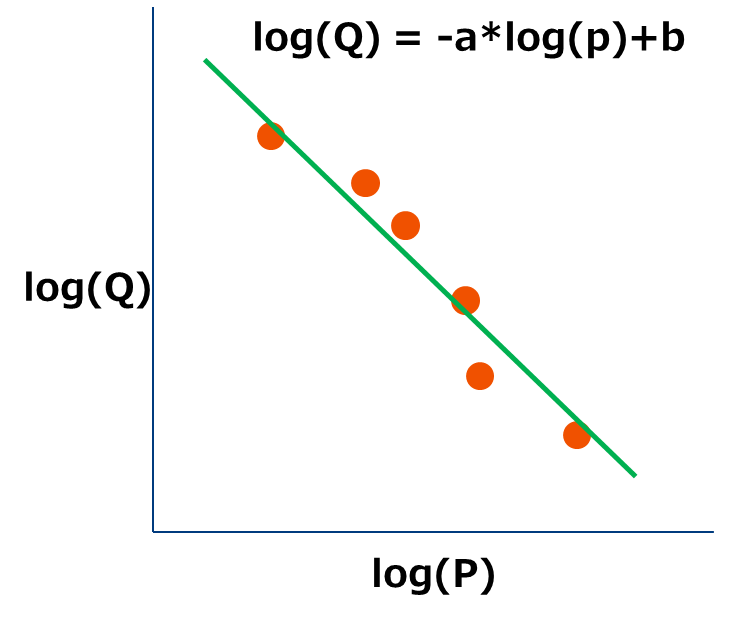
少し天下り的ですが、需要曲線が$$Q=\alpha p^{\beta} (ただし,\alpha>0,\beta<0)$$と表されるとき両辺に対数をとると、
$$ \log{Q}=\log{\alpha}+\beta\log{p} $$
logQとlogpの単回帰モデルとなります。ここで
$$ \frac{d\log{Q}}{dp} = \frac{\beta}{p} \\ \frac{d\log Q}{dQ}\frac{dQ}{dp}p = \beta \\ \frac{p}{Q}\frac{dQ}{dp} = \beta \\ $$
となり、βは弾力性に-1を乗じたものになります。つまり、この特殊なモデル式を仮定した場合に限って弾力性を求めるにはlogQとlogpの単回帰モデルのパラメータβを推定すればよいことになります。このモデルは価格弾力性が需要曲線の位置に依存しません。2.3の[例2]はα=1、β=-1の場合に相当します。
3. 実績データから逆需要曲線、弾力性を推定し、最適価格を求める
前項の議論より、実績の価格とそれに対応する需要量をもとに逆需要曲線を推定することが肝となります。
ここでは、逆需要曲線をある企業の特定のブランドに対する逆需要曲線として考えます。このように設定すると、その企業は自社の特定のブランドに対して独占的な供給者となり、価格を自由に設定することができます。
3.1 どのようなデータが必要か
さて逆需要曲線を推定するためには、少なくとも特定の期間における実際の価格と実績販売数量が必要です。具体的には以下のようなデータです。
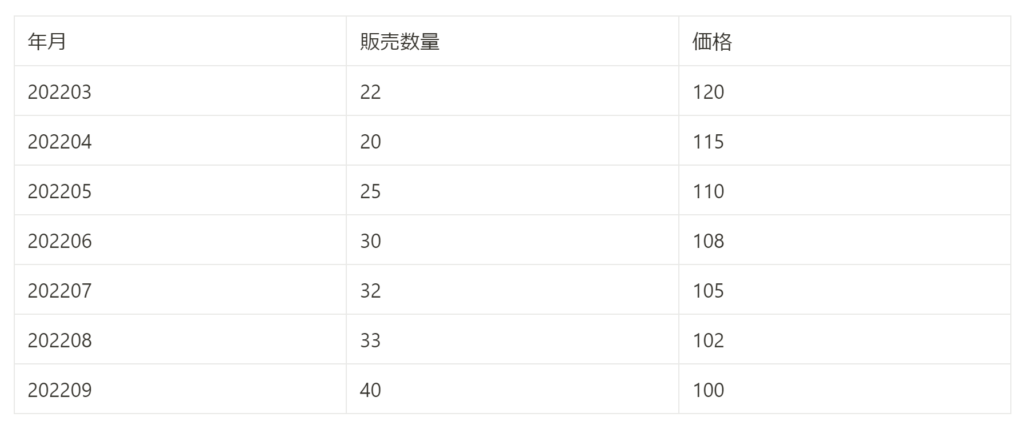
問題として適当かどうかの疑問が残りますが、ここでは販売数量を需要量の実績値としてみなします。
3.2 モデルの仮定
3.2.1 線形回帰モデル
もっともシンプルな方法です。価格を説明変数、販売数量を目的変数として線形回帰モデルを構築します。教科書の例題にも多く取り上げられています。
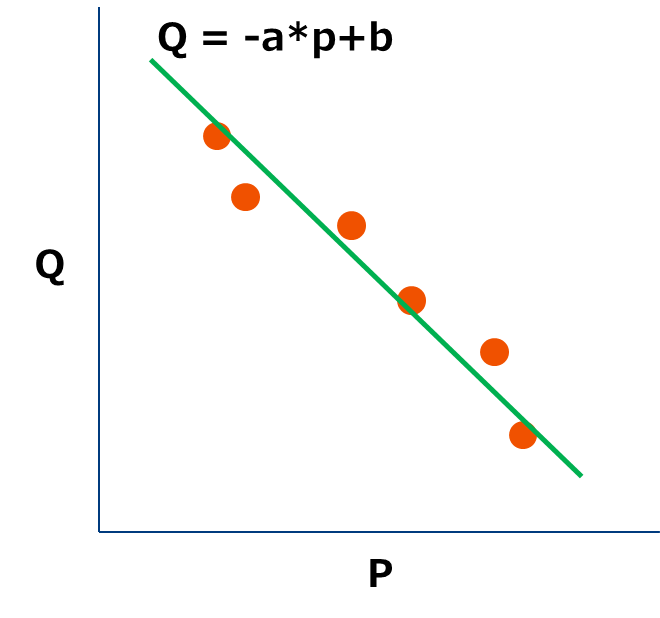
属性変数(性別・年齢)などを追加する場合は重回帰モデルを用いるか、属性ごとにグループ分けして複数の単回帰モデルを作成し、その和を推定需要曲線とします。ただし各々の単回帰モデルの定義域、つまり-a*p+b≥0を満たす区間[0,b/a]を考慮する必要があるため、その需要曲線は複数の直線がある節で繋がった屈折需要曲線になります。3この場合、最適化問題が面倒なことになるためあまりおすすめしません。また属性の構成が大きく変わったりしない場合、重回帰モデルを作る意味は乏しく、シンプルな単回帰モデルで十分です。
3.2.2 対数回帰モデル
2.4で紹介したモデルです。log(価格)を説明変数、log(販売数量)を目的変数として対数回帰モデルを構築します。このモデルは回帰係数そのものが価格弾力性となります。このことから分かるように価格によらず弾力性は一定です。つまり100円→110円の場合と、100万円→110万円の場合で需要の減少率は同じです。
3.2.3 機械学習モデル
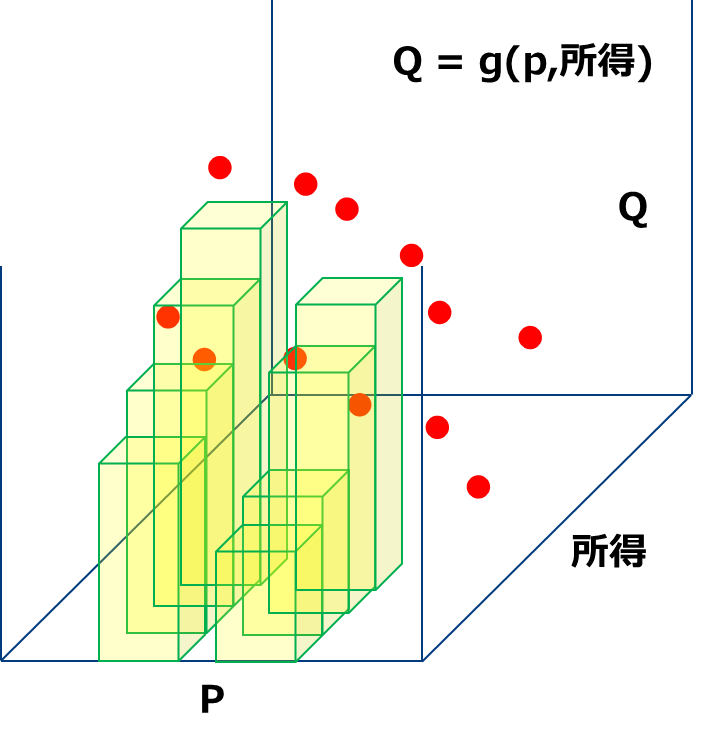
需要は価格のみで決定されるわけではないという主張に皆様も同意されるのではないでしょうか。例えば、所得の増加は同一価格での需要を増やします。また、性別や年齢などの属性の違いによって需要曲線の形状も異なるかもしれません。
このような場合最近では機械学習モデルを用います4https://thedatageneralist.com/using-machine-learning-to-estimate-price-elasticity/。このモデルは特定の回帰曲線を仮定するのではなく、とにかくQ≈f(p)となるような入出力を学習します。決定木や、それらのアンサンブルモデルが有名です。価格だけではなく、様々な要素、例えば性別・年齢・所得などのデモグラフィック変数なども説明変数として取り入れたい場合に便利です。(極端な話、消費者個人単位で購買率を推定しその和として需要を定義するということも可能です。ただし対象としている集団の属性構成が大きく変わらない場合は、3.2.1のモデルで十分です。)
ただしf(p)の具体的な形は明示することが困難であるため弾力性と需要曲線の関係が微分演算のみで対応させることができません。また価格の最適化においても、同様に微分が不可能であるため逐次最適をしていくという少々計算量的なめんどくささがあります。
さらに線形モデルと異なり、未知データ(極端に大きいまたは小さい価格のように需要曲線の端)に対して整合的な出力が得られるとは限らないなどの問題があります。
3.3 価格の最適化を行う
3.3.1 総収入関数
逆需要曲線をQ(p)とすると、総収入は価格×販売数量、つまりp*Q(p)となります。価格の最適化とは総収入を最大にするp^を求めることです。
3.3.2 仮定したモデルごとの総収入関数
3.2.1で仮定したpとQの関係が線形回帰モデルで表現できるとすると、総収入関数はp*Q(p)より
$$ R(p) = p(ap+b) \quad a<0,b>0 \\ = ap^2 + bp \\ =a\left(\frac{b}{2a} + p \right)- \frac{b^2}{4a} $$
ただし、a<0,b>0。これを最大化するpは2次曲線の極大点であるため、p^=-b/2aとなります。またこのp^は価格弾力性の絶対値が1になる点です。
3.2.2で仮定した対数線形モデルの場合、総収入関数は
$$ R(p) = p*\alpha p^{\beta} \\ =\alpha p^{\beta +1} $$
ただしα>0,β<0。R(p)はβ>-1の場合、単調増加、β<-1の場合単調減少、β=-1の場合定数です。つまり、需要が価格弾力的でない場合、価格を上げるほど総収入関数は増加し、弾力的である場合その逆になります。このモデルではp^は定まらず、現実的ではありません。
3.2.3の機械学習モデルは明示的にQ(p)を記述することができないことが多いためp*Q(p)を目的関数として最適化ソルバーで解くことになります。
4. Pythonで計算する
4.1 使用データ
こちらの記事で使用されいてる、牛肉価格とその需要量が四半期ごとに記録されているデータを使用します5https://raw.githubusercontent.com/susanli2016/Machine-Learning-with-Python/master/beef.csv。
必要なライブラリを読み込みます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
import japanize_matplotlibデータを読み込みます。
# https://towardsdatascience.com/calculating-price-elasticity-of-demand-statistical-modeling-with-python-6adb2fa7824d
df = pd.read_csv('https://raw.githubusercontent.com/susanli2016/Machine-Learning-with-Python/master/beef.csv')
print (df.shape)価格と需要の関係をplotします。
plt.rcParams['figure.figsize'] = (7,4)
# plt.rcParams['font.size'] = 14
# plt.rcParams['axes.grid'] = False
# plt.rcParams['axes.facecolor'] = 'white'
plt.scatter(df['Price'],df['Quantity'],color='blue',edgecolors='w', marker='o', alpha=0.7, s=100)
# x軸y軸の設定
plt.xlabel('Price')
plt.ylabel('Quantity')
# グラフを装飾
plt.title('Inverse Demand Function')
plt.tight_layout()
# plt.legend()
plt.show()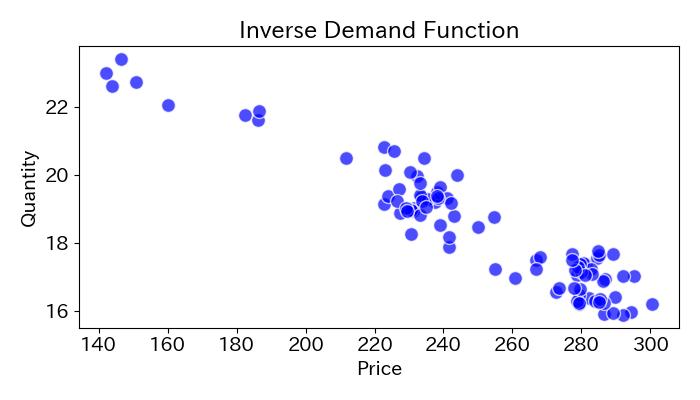
4.2 モデリングと最適化価格を求める
4.2.1 線形回帰
はじめに線形回帰モデルを試行します。statsmodelsのAPIでは切片項に相当するカラムをデータフレームに作成しておきます。
# 切片項
df['intercept'] = 1
# 線形回帰の実行
lm = sm.OLS(df['Quantity'], df[['intercept', 'Price']])
# 結果の表示
results = lm.fit()
print(results.summary())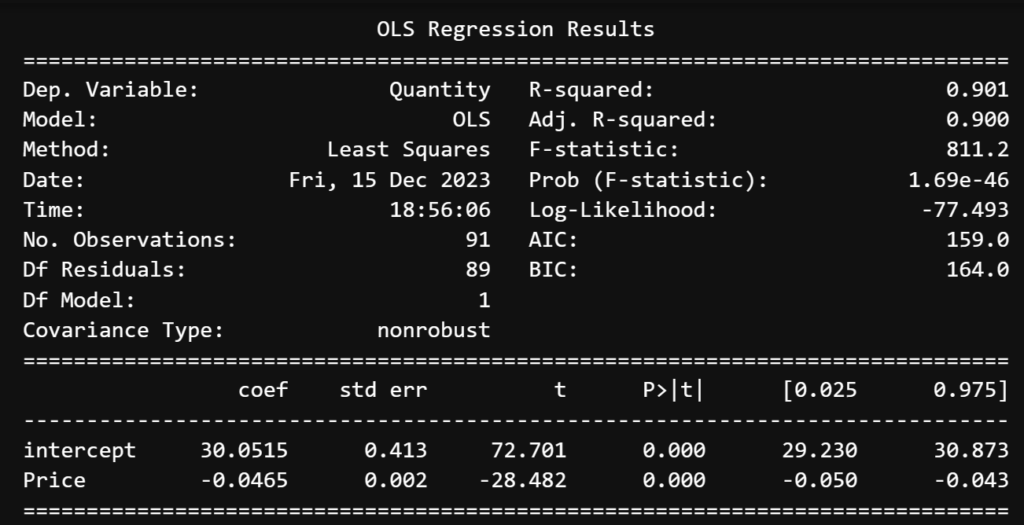
決定係数は0.9と高く、Priceと切片の係数のp値も十分小さいため、このモデルは妥当と仮定して話を進めます。推定逆需要関数は
Q = -0.0465*Price+30.051486
となります。
# 直線プロット
# y_hat = results.predict(df[['intercept', 'Price']])
intercepts = np.repeat(1, 100)
x = np.linspace(1, 400, 100)
print (intercepts)
y_hat = intercepts*results.params['intercept']+x*results.params['Price']
plt.plot(x, y_hat, color='red', label = f"推定逆需要曲線:Q = {results.params['Price']:.4f}*Price+{results.params['intercept']:4f}")
# plt.plot(df['Price'], y_hat, color='red')
plt.scatter(df['Price'],df['Quantity'],color='blue',edgecolors='w', marker='o', alpha=0.7, s=100)
# x軸y軸の設定
plt.xlabel('Price')
plt.ylabel('Quantity')
# グラフを装飾
plt.title('Inverse Demand Function')
plt.xlim(0,400)
plt.legend()
plt.tight_layout()
# plt.legend()
plt.show()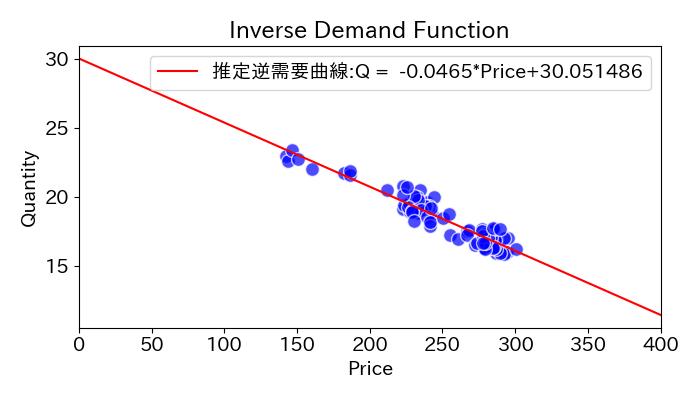
2.3より価格弾力性はPriceの値に依存しており、それをプロットすると
s = np.abs(-1/(1+(results.params['intercept']/(results.params['Price']*x))))
plt.plot(x, s, color='red')
# x軸y軸の設定
plt.xlabel('Price')
plt.ylabel('価格弾力性の絶対値')
# グラフを装飾
plt.title('Price elastic of demand')
# y = 定数 の配列を生成
y = 1 * np.ones_like(x)
# プロット
plt.plot(x, y, label=f'y = 1', color='blue', linestyle='--')
plt.xlim(0,400)
plt.tight_layout()
# plt.legend()
plt.show()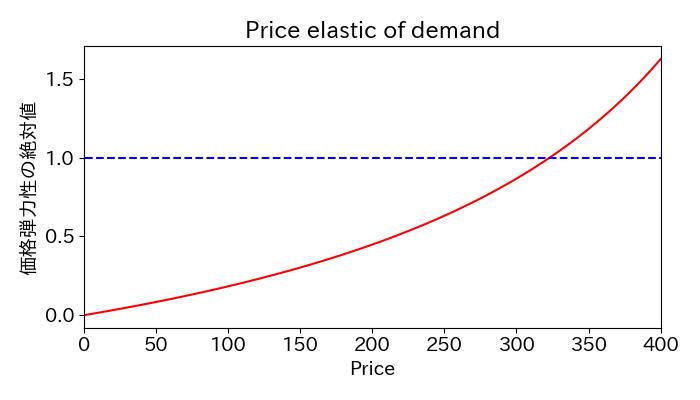
最適な価格を求める方法は2つあります。1つ目は、推定逆需要関数に価格を乗じた2次関数の最大値を求める方法です。2つ目は、価格弾力性が1となる価格を求める方法です(上図を参照)。
後者の方法で最適価格が求まる理由を簡単に説明します。価格弾力性が1より小さい場合、価格を上げると総収入が増加します。価格弾力性が1より大きい場合、価格を上げると総収入が減少します。そのため、価格弾力性が1の点で総収入が最大になります。
総収入関数が最大となる点を示します。
# 2次方程式を解く
# 2次関数の係数を設定
a = results.params['Price']
b = results.params['intercept']
c = 0
print (a,b,c)
# 最大値を求める
x_max = -b / (2 * a)
y_max = a * x_max**2 + b * x_max + c
print(f"最大値のx座標: {x_max}")
print(f"最大値のy座標: {y_max}")
# 2次関数のグラフ
intercepts = np.repeat(1, 100)
x = np.linspace(1, 400, 100)
print (intercepts)
y_hat = intercepts*results.params['intercept']+x*results.params['Price']
revenu = x * y_hat
plt.plot(x, revenu, color='red')
# y = 定数 の配列を生成
y = y_max * np.ones_like(x)
# プロット
plt.plot(x, y, label=f'y = 1', color='blue', linestyle='--')
# y値を定義
y_values = range(6000)
plt.plot([x_max] * len(y_values), y_values, color='blue', linestyle='--')
plt.xlabel('Price')
plt.ylabel('収益')
plt.text(0, y_max, f'{int(y_max)}', ha='left', va='bottom', fontsize=12)
plt.text(x_max, 0, f'{int(x_max)}', ha='left', va='bottom', fontsize=12)
plt.xlim(0)
plt.ylim(0)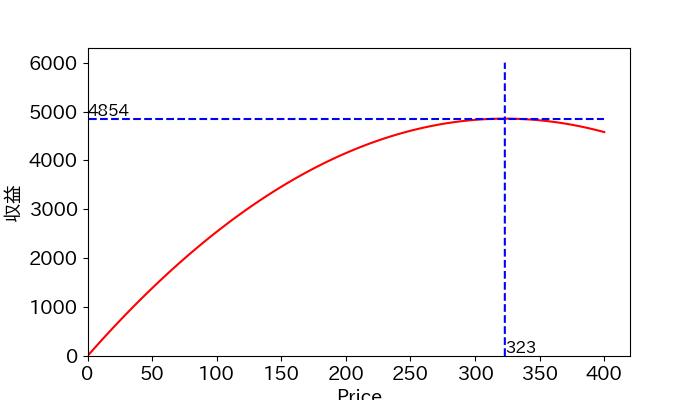
Priceが323の時に総収入が最大になります。この点は弾力性とPriceの関係図を確認すると弾力性が1となる点に対応しています。
4.2.2 対数回帰
PriceとQuantityを対数変換します。
# 対数変換
df['Price_log'] = np.log(df['Price'])
df['Quantity_log'] = np.log(df['Quantity'])
print (df)plt.rcParams['figure.figsize'] = (7,4)
plt.scatter(df['Price_log'], df['Quantity_log'], color='blue', edgecolors='w', marker='o', alpha=0.7, s=100)
# x軸y軸の設定
plt.xlabel('Price_log')
plt.ylabel('Quantity_log')
# グラフを装飾
plt.title('log-log Inverse Demand Function')
plt.tight_layout()
plt.savefig('plot_10.jpg')
plt.show()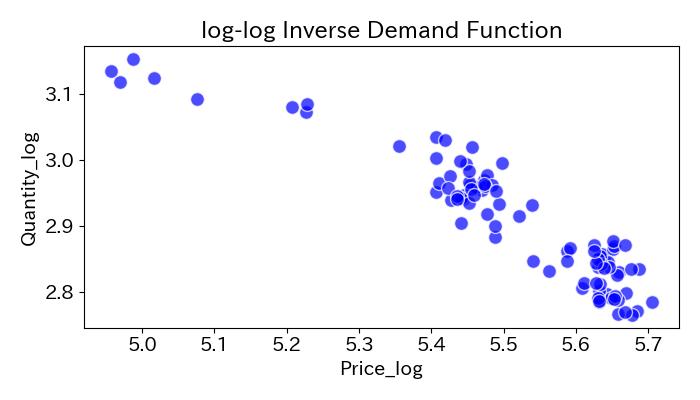
対数回帰を実行。
# 線形回帰の実行
lm = sm.OLS(df['Quantity_log'], df[['intercept', 'Price_log']])
# 結果の表示
results_log = lm.fit()
print(results_log.summary())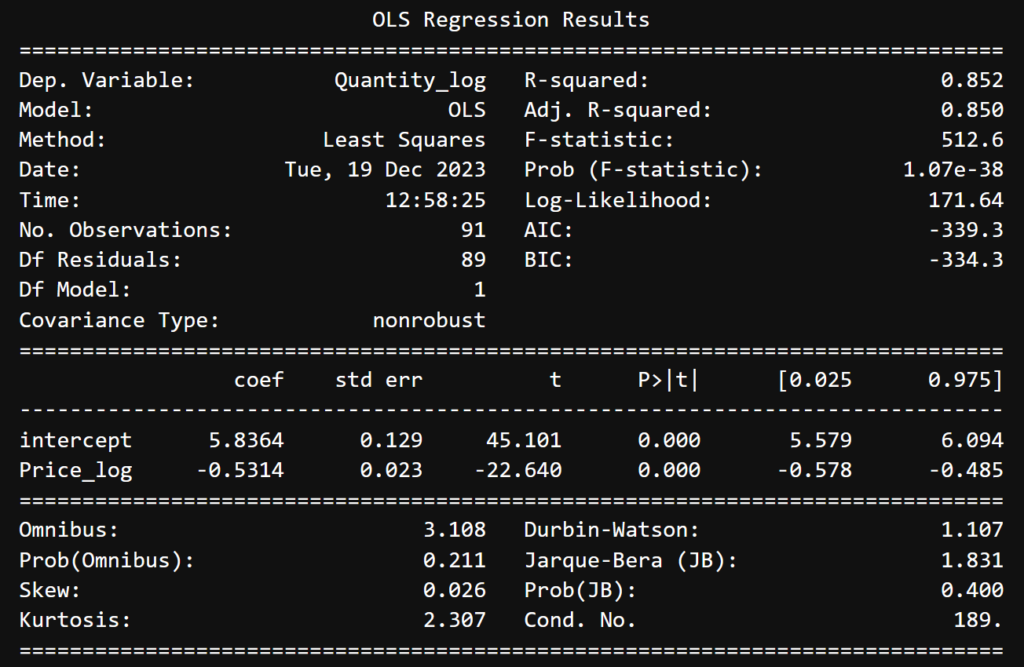
決定係数とF値、それぞれの係数のp値を確認し、適当なモデルであると仮定して話を進めます。推定逆需要曲線は
Q = Price^(-0.5314)*exp(5.836375)
となり、図示すると
# 直線プロット
y_hat = df['Price']**(results_log.params['Price_log']) * np.exp(results_log.params['intercept'])
plt.plot(df['Price'], y_hat, color='red')
plt.scatter(df['Price'],df['Quantity'],color='blue',edgecolors='w', marker='o', alpha=0.7, s=100)
# x軸y軸の設定
plt.xlabel('Price')
plt.ylabel('Quantity')
# グラフを装飾
plt.title('Inverse Demand function')
plt.tight_layout()
plt.savefig('plot_11.jpg')
plt.show()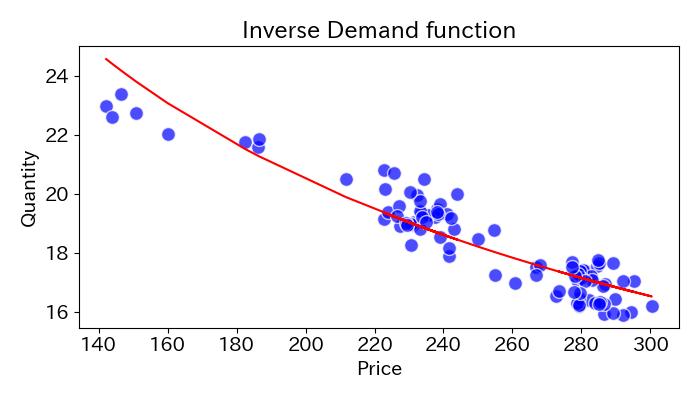
このモデルでは価格弾力性が価格に依存しない定数となります。
x = np.linspace(1, 400, 100)
s = np.abs(results_log.params['Price_log'] * np.ones_like(x))
plt.plot(x, s, color='red', label='価格弾力性')
# x軸y軸の設定
plt.xlabel('Price')
plt.ylabel('価格弾力性の絶対値')
# グラフを装飾
plt.title('Price elastic of demand')
# y = 定数 の配列を生成
y = 1 * np.ones_like(x)
# プロット
plt.plot(x, y, color='blue', linestyle='--')
plt.xlim(0,400)
plt.ylim(0,1.2)
plt.tight_layout()
plt.legend()
plt.show()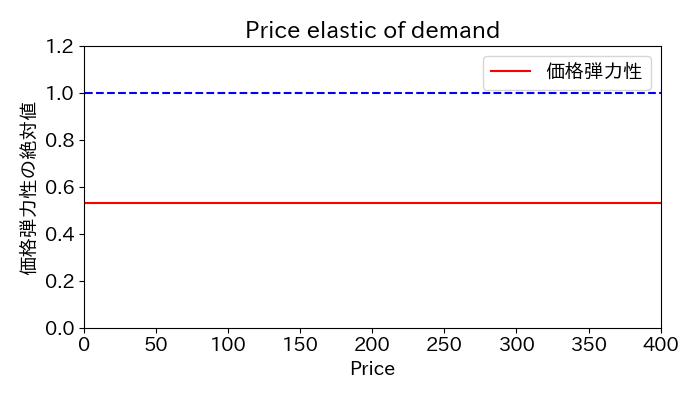
価格弾力性が常に<1であるため、総収入は価格に対して単調に増加します。
# グラフ
x = np.linspace(1, 400, 100)
y_hat = x**(results_log.params['Price_log']) * np.exp(results_log.params['intercept'])
revenu = x * y_hat
# x軸y軸の設定
plt.xlabel('Price')
plt.ylabel('総収入')
plt.plot(x, revenu, color='red')
plt.savefig('plot_13.jpg')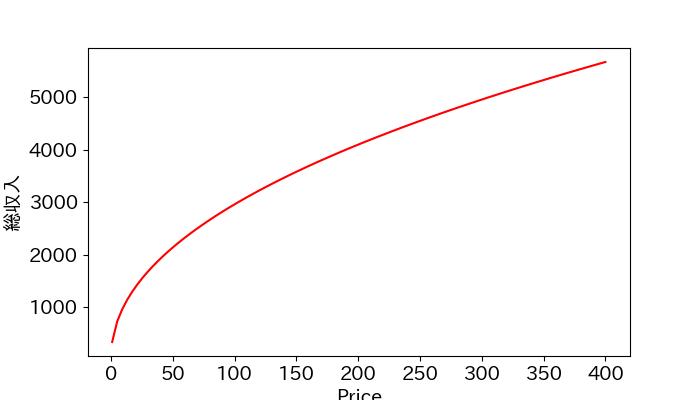
このため、最適な価格は定まりません。
機械学習モデルは今回は割愛します。
5. おわりに
価格の改定をご検討中のお客様はぜひ弊社にご相談ください。無料相談大歓迎です。ご興味ございましたら、お問い合わせはこちらから宜しくお願い致します。
[参考]
- スティーヴン・レヴィット, オースタン・グールズビー, & チャド・サイヴァーソン. (2017). レヴィット ミクロ経済学 基礎編. 東洋経済新報社.
- N・グレゴリー・マンキュー. (2019). マンキュー経済学 I ミクロ編.
- Paul J. Burke and Ashani Abayasekara The Price Elasticity of Electricity Demand in the United States https://www.jstor.org/stable/26534427?casa_token=gGDycNVMfv0AAAAA%3ALRjtMVYEgaAVhNGETlQBdNGwYeCtovepPQ8JaxaFNBEQI-C1gJ9vA_NAUoQZKenW2EpYdXoJ8WHNxoJu7n0UtN1Eidaa9gSg3EZTavdrTyXhqIBOjaM
- https://www.youtube.com/watch?v=CP-SAUS3x1Y
- https://thedatageneralist.com/using-machine-learning-to-estimate-price-elasticity/

