[想定している読者像]
生産管理の責任者、製造業の経営者の方。ベテランの方の勘と経験でスケジューリングを行ってきたが、定年退職を迎えるにあたって技術継承がうまくできていない会社の方。
[コンテンツ属性]
ビジネス:★★☆☆☆
最適化技術:★★★★☆
エンジニアリング:★★☆☆☆
製造業のDXにおいて、AIの活用と並び、最適化が重要な要素となっています。工場には様々な機械が存在し、これらの稼働時間やスケジュールは生産目標に応じて割り当てられます。一部の企業ではこれらのプロセスを自動化していますが、多くの企業ではまだベテランの実務者の感覚や経験に基づいて操作が行われています。
この記事では、最適化の問題であるジョブショップスケジューリングを取り上げ、機械との関係をモデル化し、与えられた機械と仕事(部品の目標生産数に基づいて算出された)に対して最適な機械スケジューリングを導き出します。
まず製造業においての機械スケジューリング問題について述べ、その定式化を簡単に説明します。最後に、Pythonの最適化インターフェースであるpulpと無料のソルバーを用いてこれを解きます。
1. 機械スケジューリング
1.1 製造業の4M
製造業における4Mとは、Man(人員)、Machinery (機械)、Material (材料)、Method (方法)のことです1https://www.techs-s.com/media/show/1582Favi, Claudio, Michele Germani, and Marco Marconi. “A 4M approach for a comprehensive analysis and improvement of manual assembly lines.” Procedia Manufacturing 11 (2017): 1510-1518.。これらのマネジメントを行うことで生産性の向上を目指します。本記事では特に「Machinery (機械)」に注目します。
1.2 機械のタイムマネジメント
製造業において工場内にあるものの多くは仕掛品です。これらが滞留する時間が長くなるほどキャッシュフローが悪化するため、機械に対してのタイムマネジメントは重要です。従って単位時間当たりの生産量がより大きい機械の導入や、保守性や信頼性、可用性の向上のための保全活動、3https://monoist.itmedia.co.jp/mn/articles/2203/22/news012_4.html、生産計画に応じた機械のスケジューリングを行います。
1.3 機械スケジューリング問題
機械スケジューリングとは、いつどの機械にどの仕事をさせるか計画することです4https://turbine.kuee.kyoto-u.ac.jp/~tanaka/scheduling/index.html。機械スケジューリング問題とは、ある指標を最適にする(例えば全ての仕事を最も短時間で終えるなど)ためのスケジュールを求める問題です。
スケジュールは、縦軸を「機械」、横軸を「時間」、棒グラフの構成要素を「仕事」とすると、以下のようなガントチャートで表現されます。

先行研究をもとに「機械」「仕事」の特徴及び最適化基準を整理します。5Brucker, P. (1999). Scheduling algorithms. Journal of the Operational Research Society, 50, 774-774. Springer.6Graham, Ronald Lewis, et al. “Optimization and approximation in deterministic sequencing and scheduling: a survey.” Annals of discrete mathematics. Vol. 5. Elsevier, 1979. 287-326.
仕事は以下で特徴づけられます。
- 仕事を構成するオペレーションの数(通常は1つ以上のオペレーションで構成)
- 仕事間に順序が存在するかどうか
- リリースタイムや納期
また、機械は以下で特徴づけられます。
- 単一か並列で、つまり1台の機械か複数の機械でそれぞれの仕事を処理するかどうか
- 並列の場合、同一の機械か異なる機械か
- フローショップ型(全ての仕事で使用する機械の順番が同じ)かジョブショップ型(仕事により使用する機械の順番が異なる)か
上記特徴と最適化基準を与えることで機械スケジューリング問題を定式化します。最適化する値は、様々なものがありますが、本記事ではmakespan(全ての仕事が完了するまでに要する総時間)とし、それを最小化する問題を考えます。
1.4 解法
2機械で仕事ごとに使用する機械の順番固定されている、フローショップ型生産法に関してはmakespanを最小化するジョンソン法という簡単なアルゴリズムが知られています。しかし実務ではこのような簡単な設定であるある場合は稀であり、実用性に欠けるという意見があります。7タイム・コンサルタントの日誌から https://brevis.exblog.jp/29607035/
より複雑なジョブショップ型スケジューリング問題に対してはオペレーションズ・リサーチの手法を用いた組み合わせ最適化手法が提案されています。ジョブショップ型スケジューリングの最適化は①ジョブごとにオペレーションの順番が決まっており、その順番で処理をする必要がある。②同一時刻に同じ機械で別のオペレーションを実行することはできない、この制約のもとでmakespanを最小化します。これは混合整数計画問題で定式化できます(樋野 励 [2017])8ジョブショップスケジューリング問題の数理表現 https://www.jstage.jst.go.jp/article/isciesci/61/1/61_14/_pdf/-char/ja 。
2. 問題の定式化
本節では、ジョブショップ型の混合整数計画問題の定式化について簡単に説明します。詳細にご興味がない方は、この部分をスキップし、「3.実践」を先にご覧いただくことも可能です。簡単のため「納期」「利用可能時間」をなしにして考えます。
2.1 記号
- 仕事の集合:\(J=\{1,2,…,N_{J}\}\)
- 機械の集合: \(M=\{1,2,…,N_{M}\}\)
- 任意の仕事\(j \in J \)は処理するオペレーションの順番を持ち、それは\(\{\sigma_{1}^j,…,\sigma_{k}^j\}\)という集合で表現できる。また問題を簡単にするため、1つのオペレーションに1つの機械が対応する、つまり\(\sigma_{i}^j \in M \) が成立するように仮定します。例えばある仕事に対してのオペレーション集合が{4,2,3,1}であるならばその仕事は機械4、機械2、機械3、機械1の順番で処理する必要があります。
- \(x_{mj} \geq 0\):機械mで仕事jの作業を開始する時間
- \(p_{mj} \geq 0\):機械mで仕事jの作業を実行する時間
- \(z_{mjk} \in \{0,1\}\):機械mで仕事jの作業を仕事kより先に行う場合1、それ以外0をとる変数
- C:最小化するmakespan
2.2 定式化
まずmakespanを最小化するので目的関数は
$$min\quad C$$
制約条件はまず各仕事は与えらえた順序で処理されなければならないため
$$x_{\sigma_{h-1}^jj} + p_{\sigma_{h-1}^jj} \leq x_{\sigma_{h}^jj} \quad \forall j \in J,\forall h\in\{2,…,N_{M}\}$$
同一時間、同一機械で異なる仕事の作業はできないため
$$x_{mj} + p_{mj} \leq x_{mk} + V(1-z_{mjk})\quad j,k \in J,j \neq k,m\in M$$
右辺の第二項は、jとkの作業順序が前後しても制約を満たすために必要な項です。Vは適当に大きな値を割り当てます。これはビッグM法というテクニックですが、Mとしてしまうと機械の集合と同じ記号になってしまうため、Vとしています。
jとkの作業順は「j→k」、「k→j」のいずれかを満たすので
$$z_{mjk} + z_{mkj} =1 \quad j,k \in J, j \neq k, m \in M$$
仕事の順番が割当られている場合、このzは定数、割当られていない場合(つまり順番は問わない)、0 or 1 をとる変数となります。
makespanは全ての仕事が終わる時間でしたので
$$x_{\sigma_{|M|}^jj} + p_{\sigma_{|M|}^jj} \leq C \quad j \in J$$
以上をまとめると。
$$min\quad C \\ x_{\sigma_{h-1}^jj} + p_{\sigma_{h-1}^jj} \leq x_{\sigma_{h}^jj} \quad j \in J,h\in\{2,…,N_{M}\} \\ x_{mj} + p_{mj} \leq x_{mk} + V(1-z_{mjk})\quad j,k \in J,j \neq k,m\in M \\ z_{mjk} + z_{mkj} =1 \quad j,k \in J, j \neq k, m \in M \\ x_{\sigma_{|M|}^jj} + p_{\sigma_{|M|}^jj} \leq C \quad j \in J$$
です。主にこちらを参照しました。
Bruno Scalia C. F. Leite The Job-Shop Scheduling Problem: Mixed-Integer Programming Models https://medium.com/towards-data-science/the-job-shop-scheduling-problem-mixed-integer-programming-models-4bbee83d16ab
3. 実践ジョブショップスケジューリング問題
本節では疑似的に与えられた機械や仕事の特性からmakespanを最適にする問題の実践を行います。
3.1 架空の問題
ある3種類の製品を作成するために、5つの機械で作成する問題を考えます。製品ごとに作業する機械の順番と、作業時間が与えられています。ただし製品1は4つの機械の作業だけで作成します。
| 順番1 | 順番2 | 順番3 | 順番4 | 順番5 | |
|---|---|---|---|---|---|
| 製品0 | 機械0:90分 | 機械4:120分 | 機械2:60分 | 機械3:80分 | 機械1:50分 |
| 製品1 | 機械2:120分 | 機械0:100分 | 機械4:80分 | 機械1:50分 | 機械3:0分 |
| 製品2 | 機械1:80分 | 機械2:70分 | 機械3:70分 | 機械4:40分 | 機械0:50分 |
製品1は機械3を使用しないため、機械3は0分としてあります。また製品作成の順序は問いません。製品iを作成することを仕事iとします。
3.2 pythonインターフェースとソルバー
これら与えらえた問題をソルバーで解くためにpythonのplupというインターフェースを用いて定式化します。ソルバーは計算エンジンでインターフェースは問題を記述しエンジンに渡すものと考えて頂ければ結構です。
pulpのインストールはpythonの適当(anacondaなど)な環境で行います。
pip install pulppulpをインストールするとデフォルトで無料のCBCソルバーを利用できます。なおGurobi Optimizer9https://www.gurobi.com/solutions/gurobi-optimizer/などの有料のソルバーにも接続が可能です。
3.3 いざ実行
pulpライブライリをimportします。pulpは線形計画問題に対応しています。
# 必要なライブラリをインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import pulp # 線形計画法を使用するためのPuLPモジュールをインポート3.1で設定した問題を以下のように定義します。
# 定数を与える
# 機械数
M = 5
# 仕事数
J = 3
# 仕事辞書作成
J_dic = {}
J_dic[0] = {0:90,4:120,2:60,3:80,1:50}
J_dic[1] = {2:120,0:100,4:80,1:50,3:0}
J_dic[2] = {1:80,2:70,3:70,4:40,0:50}
# 稼働時間行列作成
P = np.array([J_dic[j][m] for m in range(M) for j in range(J)]).reshape(M,J)
# BIG M
V = 1.0e5問題を定式化します。
# モデルを作成
model = pulp.LpProblem("Optimization Problem", pulp.LpMinimize)
# xmjの定義
x = pulp.LpVariable.dicts("x", ((m, j) for m in range(M) for j in range(J)), lowBound=0, cat="Continuous")
# makespan変数の定義
C = pulp.LpVariable("C", lowBound=0, cat="Continuous")
# zmjk(バイナリ変数)の定義
z = pulp.LpVariable.dicts("z", ((m, j, k) for m in range(M) for j in range(J) for k in range(J)), cat="Binary")
# 目的関数を設定
model += C
# 制約条件を追加
# 制約条件0: 各ジョブが前のジョブが終了した後に始まる
for j in range(J):
for h in range(1, M):
sigma = list(J_dic[j].keys())
constraint_expr = x[(sigma[h - 1], j)] + P[(sigma[h - 1], j)] <= x[(sigma[h], j)]
model += constraint_expr, f"constraint0_{j}_{h}"
# 制約条件1: ジョブの処理が重ならない
for j in range(J):
for k in range(J):
for m in range(M):
if j != k:
constraint_expr = x[(m, j)] + P[(m, j)] <= x[(m, k)] + V * (1 - z[(m, j, k)])
model += constraint_expr, f"constraint1_{j}_{k}_{m}"
# 制約条件2: 仕事の順番の制約
for j in range(J):
for k in range(J):
for m in range(M):
if j != k:
constraint_expr = z[(m, j, k)] + z[(m, k, j)] == 1
model += constraint_expr, f"constraint2_{j}_{k}_{m}"
# 制約条件3: 各ジョブは最終的にCよりも遅れない
for j in range(J):
sigma = list(J_dic[j].keys())
constraint_expr = x[(sigma[M - 1], j)] + P[(sigma[M - 1], j)] <= C
model += constraint_expr, f"constraint3_{j}"
# 最適化問題を解く
model.solve(solver=pulp.PULP_CBC_CMD()) # PuLPを使用して問題を解く解をスケジュール表にしてみましょう。午前8時始業とします。
# plt.figure(figsize=(14,7))
# スタート時間を定義(午前8時)
start_time = 8 * 60
# バーの色のリスト
colors = ['red', 'green', 'blue']
labels = [f"Job_{i}" for i in range(J)]
indexes = [f"Machine_{m}" for m in range(M)]
# グラフを描画
for j in range(J):
plt.barh(indexes, P[:,j], left=sol[:,j] + start_time, color=colors[j], label=labels[j], height=1)
# グラフの設定
plt.xlabel('Time (Minutes)')
plt.ylabel('Machine')
plt.xticks(np.arange(480, 10*60 + 481, 60), [f"{hour:02d}:00" for hour in range(8, 19)])
plt.title('Job Schedule Starting from 8:00 AM')
plt.legend()
# 縦軸のグリッドを消す
plt.grid(True, axis='x') # x軸に対してのみグリッドを描画
plt.grid(False, axis='y') # y軸に対してグリッドを描画しない
# グラフを表示
plt.show()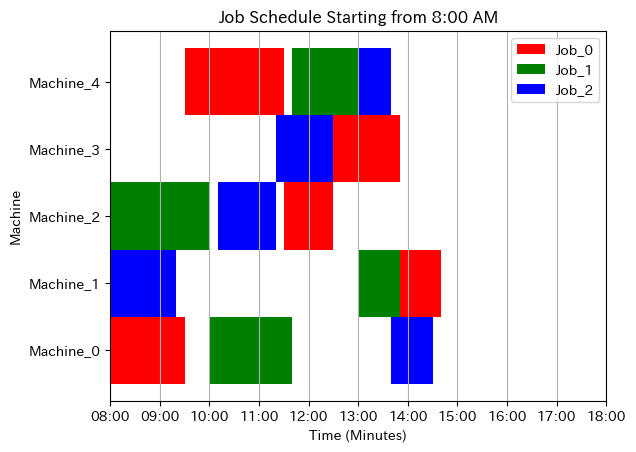
このままですと、お昼休み仕事をしなければなないため、お昼は一時中断するようにします。この場合
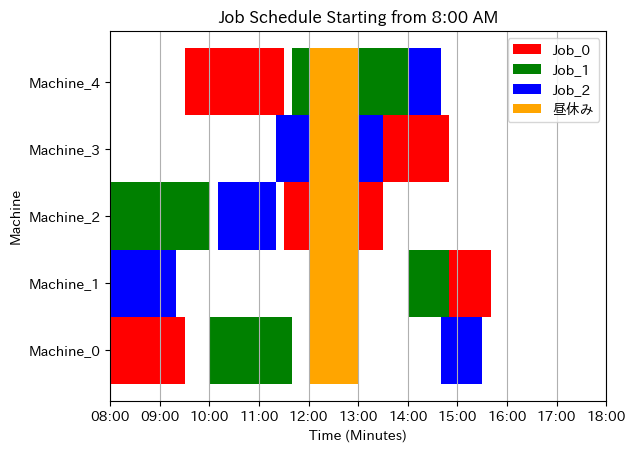
となります。以下はお昼休みを表示するためのコードです。機械をアイドルさせてお昼休みに入るかどうかは実務的なすり合わせが必要です。
start_time = 8 * 60
data = sol + start_time + P
P1 = P - (data - np.minimum(data,720))
bools1 = P1 < 0
bools2 = P1 >= 0
P1[bools1] = 0
P2 = P.copy()
P2[data < 720] = 0
P3 = P2 - P1
P3[P3<0] = 0
p_l = np.ones(5)*60
s_l = np.ones(5)*720
# plt.figure(figsize=(14,7))
# スタート時間を定義(午前8時)
# バーの色のリスト
colors = ['red', 'green', 'blue']
labels = [f"Job_{i}" for i in range(J)]
indexes = [f"Machine_{m}" for m in range(M)]
# グラフを描画
for j in range(J):
plt.barh(indexes, P1[:,j], left=sol[:,j] + start_time, color=colors[j], label=labels[j], height=1)
# グラフを描画
for j in range(J):
plt.barh(indexes, P3[:,j], left=np.maximum(sol[:,j] + start_time + 60,780), color=colors[j], height=1)
# グラフを描画
plt.barh(indexes, p_l, left=s_l, color='Orange', label='昼休み',height=1)
# グラフの設定
plt.xlabel('Time (Minutes)')
plt.ylabel('Machine')
plt.xticks(np.arange(480, 10*60 + 481, 60), [f"{hour:02d}:00" for hour in range(8, 19)])
plt.title('Job Schedule Starting from 8:00 AM')
plt.legend()
# 縦軸のグリッドを消す
plt.grid(True, axis='x') # x軸に対してのみグリッドを描画
plt.grid(False, axis='y') # y軸に対してグリッドを描画しない
# グラフを表示
plt.show()
4. まとめ
本記事では複数機械における順不同仕事(ただし仕事の各オペレーションは順序あり)に対してmakespanを最小化する問題を混合整数計画法で解きました。
実際の工場ではもっと複雑で変数の多い問題を扱う必要がります。最適化に関しては是非弊社までお問合せ頂けますと幸いでございます。
無料相談大歓迎です。ご興味ございましたら、お問い合わせはこちらから宜しくお願い致します。

