久しぶりに分析実務に関わる話を書きます。内容は回帰分析やロジスティクス回帰などの線形モデルを扱うときに重要な外れ値の処理です。対象読者は
- 売上予測などを線形回帰モデルで行いたい人。
- 外れ値が多いデータの取り扱いを知りたい人。
- 線形モデルを業務運用に用いたい人。
を想定しています。
外れ値が与える影響
外れ値は分布の中心から大きく外れた値です。厳密な定義があるわけではないですが、例えば数年に一度あるかないかの真夏日だとか、年間に来店回数が300日の顧客だとかが実務では外れ値として扱うことが多いです。
この外れ値は線形回帰やロジスティクス回帰などの線形モデルの推定に悪影響を与えることがあります。以下の例でみてみましょう。左の図(外れ値がない)から意図的に外れ値を作成したデータが右図です。
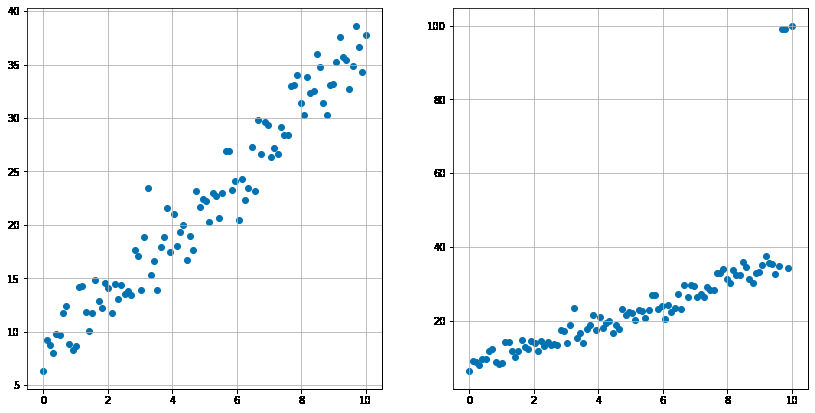
直線を当てはめてみます。
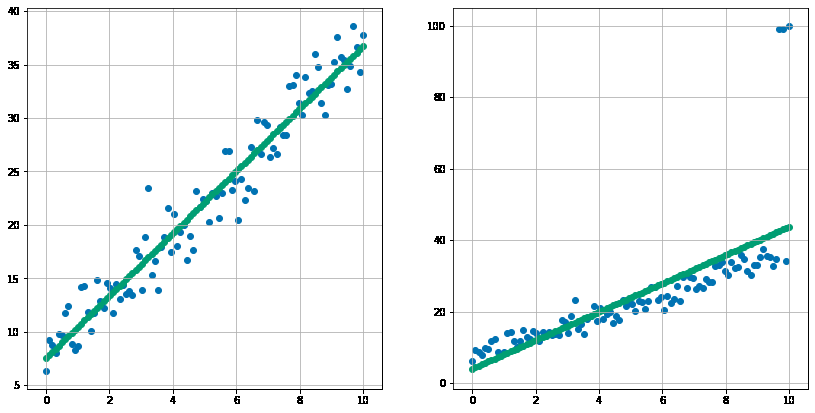
右の図の緑のと左の線を比較してみると、右図の左の線がやや上振れしているのがわかると思います。このように外れ値は少数でもモデルに影響を与えバイアスを生じさせている事がわかります。
処理の方法ではなく外れ値処理を行う対象を整理する
元来古典的な統計学の世界では回帰モデルやそれに準ずる手法は、データの説明や解釈の用途に重きをおいてきました。一方でスコアリングの実装の容易さから予測に用いられることも当然あります。この際予測用のデータに訓練データと同じ処理をすべきか、またはすべきなのに実装フェーズでは忘れらているのではないのか?という問いが筆者の問題意識としてありました。よく見かけた例が
- 学習データで外れ値を除外してモデルを作成した。実際にスコアリングする新たなデータでも同じように除外してしまっている。そのため分布の端っこのデータに予測値が付与されない。
- 学習データで99%タイルで外れ値を丸めたが、新しいスコアリングするデータで処理する際その99%タイル(すなわち学習データを丸めた時の閾値と異なる値で丸めてしまっている)で外れ値を丸めてしまった。または外れ値処理を新しいデータには行っていない。
- 学習データのターゲット変数に外れ値処理を行い、検証データでも外れ値処理を行い精度を測定してしまっている。(実際に新しくスコアリングするデータにターゲット変数はないため検証になっていない)
などです。上記は専門家でも油断しているとやりかねない、またはどれが本当に正しいのかよくわかっていないということがあります。本稿では外れ値処理の対象ごとのパターンを整理し、どれが一番妥当なのかを検証します。
処理パターンは除去と代入、そしてその対象として訓練・検証データ、説明変数・ターゲット変数の軸で以下のように分けました。なお代入は5%タイル点より小さいものは5%タイル点を、95%タイル点より大きいもは95%タイル点の値を代入しています。
githubにもあげていますが、自作の丸め代入関数を記載しておきます。
#丸目関数作成
def roundout(col,pct,train_col):
pct_low = np.percentile(train_col,pct)
pct_high = np.percentile(train_col,100-pct)
col[col<pct_low] = pct_low
col[col>pct_high] = pct_high
return (col)
対象データセットはscikit-learn.datasetsのボストンの住宅価格データ、モデルは線形回帰です。データセットやモデル詳細には立ち入りませんので、興味のある方は調べてください。外れ値処理の対象変数はターゲット変数を含めた5変数です。
検証結果
結果は以下の通りでした。尚精度はRMSEです。何もしない場合と比較し、除去する場合の精度は著しく良いです。一方でこれは当てにくいところを落としているからともいえます。2-123で比較すると、説明変数・ターゲット変数双方に処理を行い、検証データでも説明変数に処理を施したものが一番良い結果となっています。
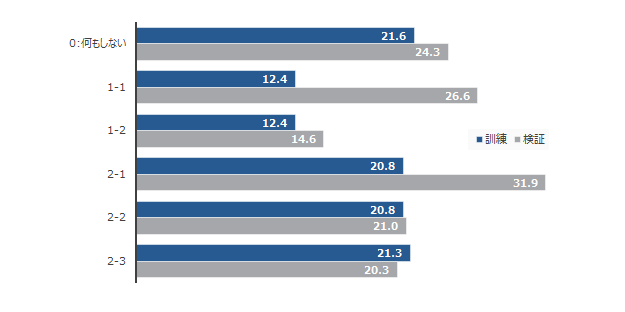
上記の結果から、直観に反せずかつ運用も容易な2-3を採択するとよさそうです。

