lightweightMMM(lw3m)の説明及び基本的な使い方はこちらをご参照ください。本章では今までの記事で解説できなかった、lw3mの応用を解説していきます。
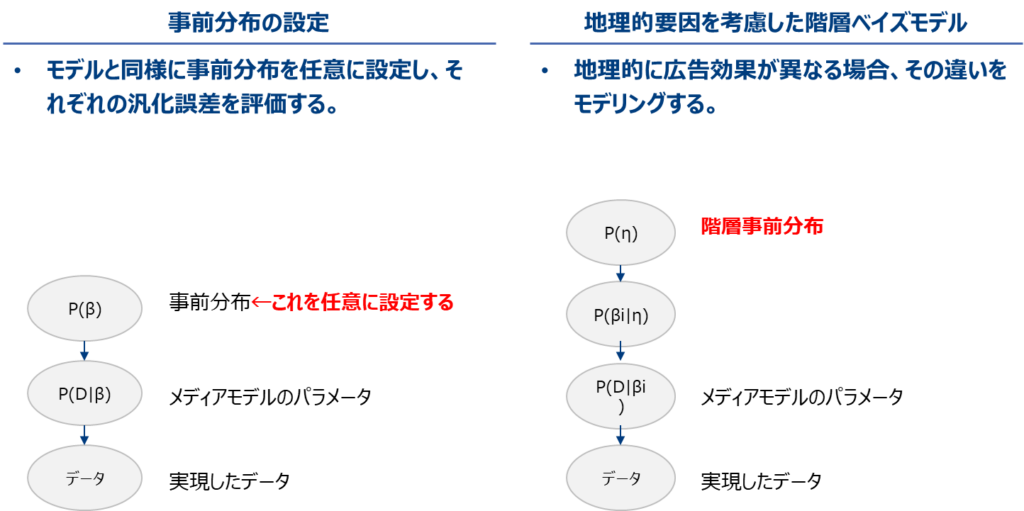
lw3mには基本機能に加えて、①任意に設定できる事前分布を使用する機能や、②地域的要因を考慮した階層ベイズモデルに対応した機能があります。
lw3mはベイズモデルであるため、事後分布は尤度と事前分布の積に比例します。データが多ければ事前分布からの影響は少ないのですが、そうでない場合は事前分布の設定にモデルが影響を受けます。lw3mは任意の分布を事前分布として設定することができます。どの分布が良いかというのはこの記事のレベルを超えるため、興味がある方は専門書をご覧ください。1東工大 渡辺澄夫研究室 HP http://watanabe-www.math.dis.titech.ac.jp/users/swatanab/prior.html
次に地域的要因をモデルに組み込む機能について説明します。これは地域間の違いを階層ベイズモデルで表現します。階層ベイズモデルとは事前分布の事前分布(超事前分布という)を導入したモデルであり、地域間の異質性と同質性をモデリングします。何言っているか分かりにくいと思いますが、要するに「地域特性=全体の平均的傾向+地域ごとの全体平均からの乖離」という仮定を考え、地域の特徴を考慮しますということです。
上記2つの解説に加えて本稿では、③lw3mのちょっとしたグラフの表記のtipsや、④MMMの留意点などを簡単に解説します。
ベイズ推定に関しては、慎重に調査し、書いていますが間違っている可能性もあります。お気づきの点ございましたらご指摘いただければ幸いです。
① 事前分布を設定する
lw3mはベイズ回帰モデルであるため、係数パラメータなどを事後分布からサンプリングして推定量を求めます。事後分布は尤度と事前分布の積に比例するため、あらかじめ事前分布を設定項目として与える必要があります。
$$ 推定量 \hat{y}=α(切片)+β1*TV投下量+β2*GDN投下量+γ*周期項+σ(誤差分散) $$
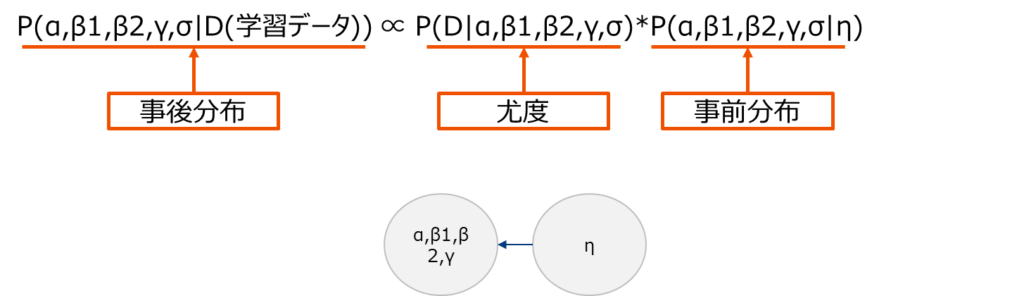
データ量が多い場合、事前分布の影響はほぼ消えるため、そこまで気にする必要はないとされています2とされるが最近の研究では、事前分布の適当さを評価する研究もあるよう。一般的に、幅の広い分布(無情報事前分布)や、計算しやすい分布(共役事前分布)が選ばれやすい。。しかし、データ量が少ない場合、その影響を受けるます。つまり設定項目の任意性が結果に影響を与えるということです。
lw3mでは事前分布を指定しないとデフォルトで以下の分布が適用されます。そのため問題によっては不適当な場合があります。3メディアの重み係数のみ指定ができない。これは与えたデータによって定まる仕様であるから。
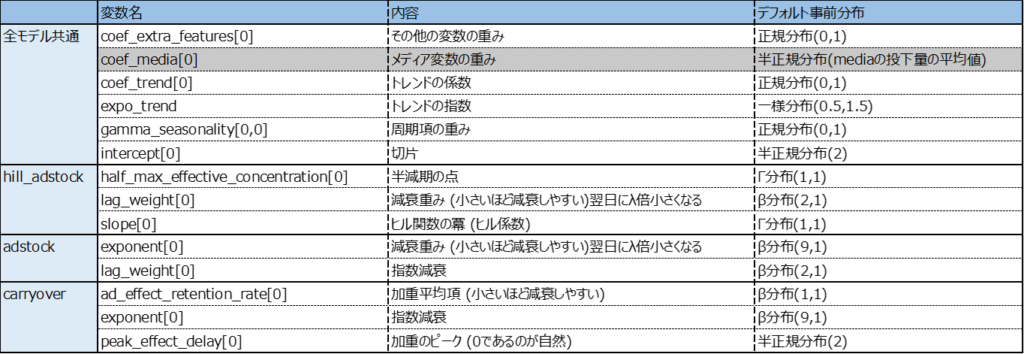
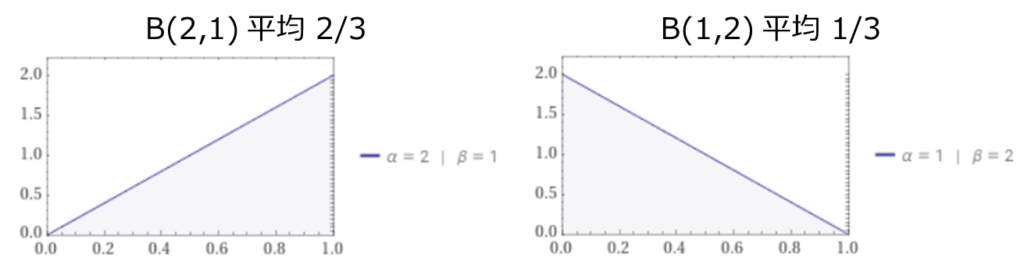
過去の実績から広告の減衰が毎日約30%と分かっている場合などは、それに近い事前分布を与えることでデータの少なさを補うことが期待されます。例えばデフォルトのlag_weithtの事前分布β(2,1)を使うより、β(1,2)を使う方が経験上の値に近い値が得られそうです。
事前分布の設定は以下のように行います。モデル構築時に引数custom_priorsに任意の分布を辞書形式で渡します。
%%time
number_warmup=2000
number_samples=2000
# For replicability in terms of random number generation in sampling
# reuse the same seed for different trainings.
mmm.fit(
media=media_data_train_scale,
media_prior=costs_scale,
target=target_train_scale,
extra_features=extra_features_train,
number_warmup=number_warmup,
number_samples=number_samples,
number_chains=N_CHAINS,
seasonality_frequency=52,# 日次データの場合365として以下の変数のコメントアウトをはずす
# weekday_seasonality=True,
custom_priors={ "intercept": numpyro.distributions.Normal(loc=0, scale=1),# 切片(ベースライン)
"coef_trend": numpyro.distributions.Normal(loc=2, scale=1),# トレンドの係数
"expo_trend": numpyro.distributions.Uniform(low=1.0, high=3.5),# トレンドの指数
"gamma_seasonality": numpyro.distributions.Normal(loc=1, scale=1),# 周期項の重み
"coef_extra_features": numpyro.distributions.Normal(loc=-5, scale=0.1),# その他の変数の重み
"half_max_effective_concentration": numpyro.distributions.Gamma(concentration=2., rate=1.),# 半減期の点
"slope": numpyro.distributions.Gamma(concentration=2., rate=1.),# ヒル関数の冪 (ヒル係数)
"lag_weight": numpyro.distributions.Beta(concentration1=3., concentration0=1.),# 減衰重み (小さいほど減衰しやすい)翌日にλ倍小さくなる
},
seed=SEED)
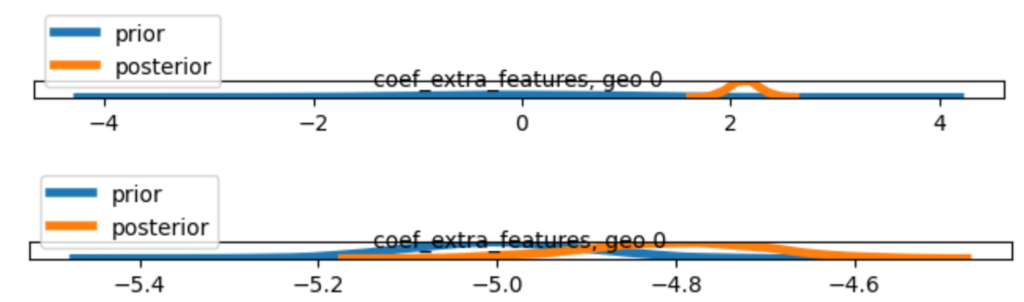
極端な事前分布を設定した場合、結果がおかしくなる例を以下で確認します。
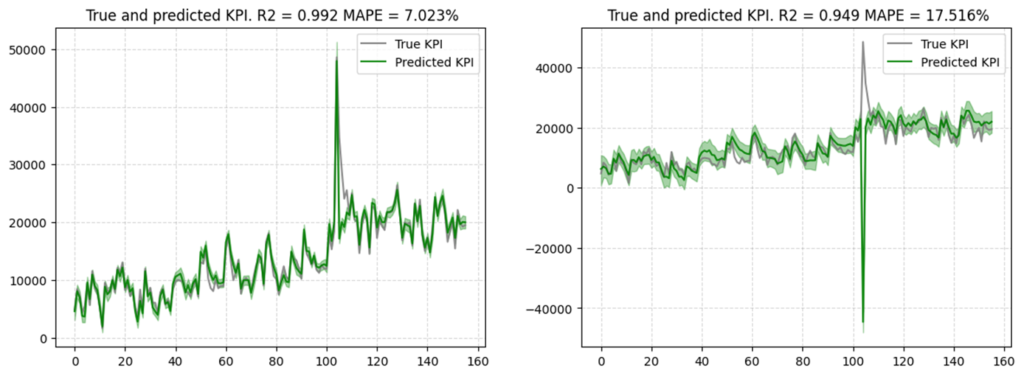
引数に渡す分布のリストは以下の通りです。

② GEO階層モデル
地理的要因により広告が与える影響が異なる場合、首都圏、関西のデータを一つのデータとしてモデリングすると、この違いを補足できません。
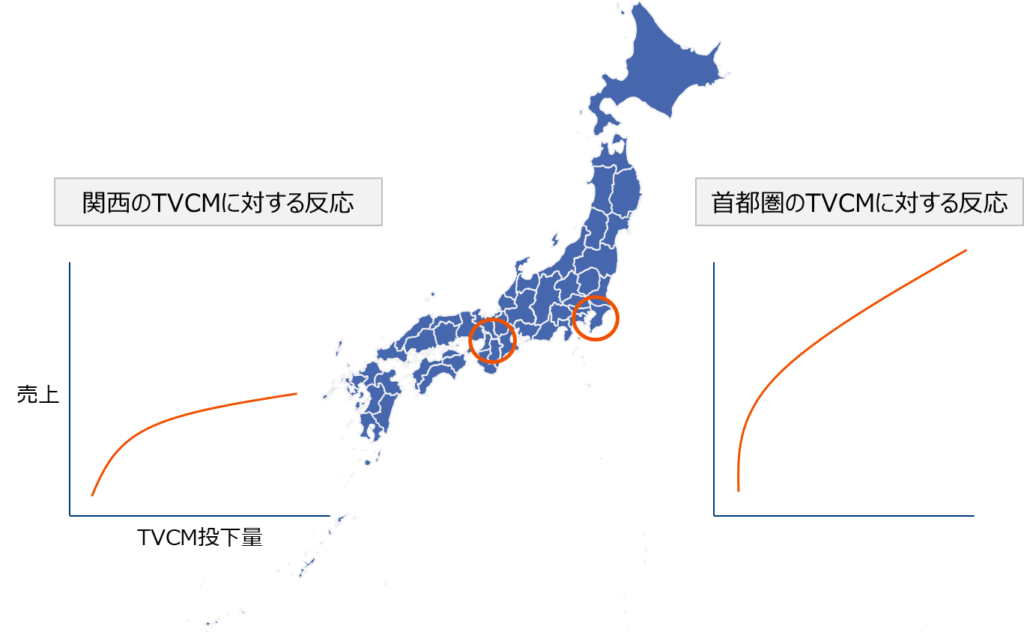
これに対して、ダミー変数法やデータを分割してそれぞれにモデリングする方法などがありますが、lw3mは階層ベイズモデルを用いた方法を提供しています。

ざっくり言うとデータが少ない地域は、足りない情報量を全体から借りてくるイメージ。
理屈はややこしいですが、lw3mでの実践は簡単。地域ごとに分割したデータを用意し、縦横地域数の配列に変換し、それを入力として従来のやりかたと同じようにモデリングするだけです。
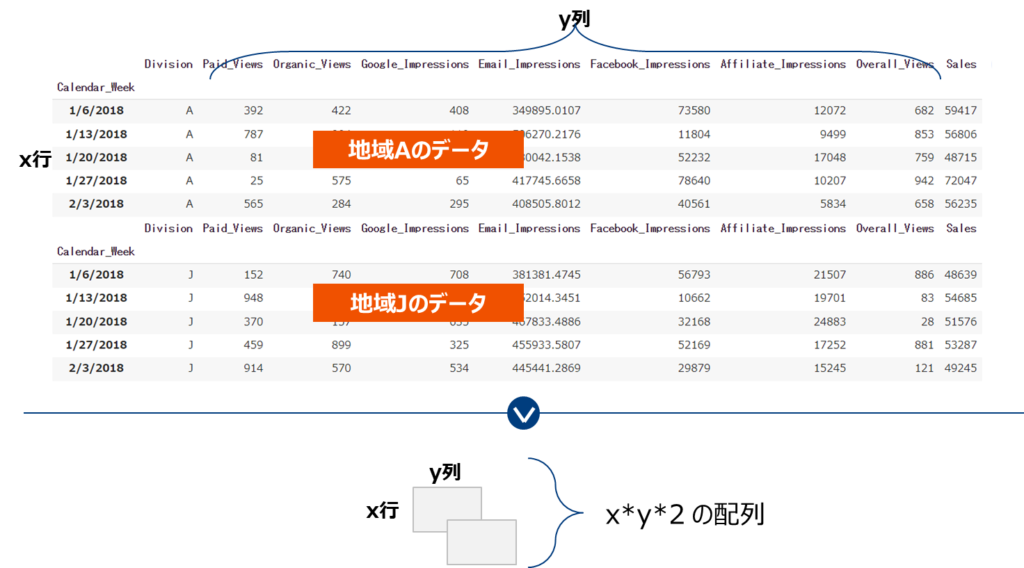
以降は通常のlightweightMMMとほぼ同じです。一応コードを記載します。なお必要なライブラリはインストール済かつimport済とします。
サンプルデータはkaggleのhttps://www.kaggle.com/datasets/yugagrawal95/sample-media-spends-data このデータを使用します。
②-1 データ読込
SEED = 12345
df = pd.read_csv('Sample Media Spend Data.csv').set_index('Calendar_Week')
df_A = df[df['Division']=='A']
df_B = df[df['Division']=='J']
②-2 xy()地域数の配列に変換
media_cols = ['Paid_Views', 'Google_Impressions', 'Facebook_Impressions', 'Affiliate_Impressions', 'Overall_Views']
extra_cols = ['Email_Impressions']
# メディアデータ
media_data = np.dstack((df_A[media_cols].values, df_B[media_cols].values))
# extraデータ
extra_features = np.dstack((df_A[extra_cols].values, df_B[extra_cols].values))
# 総コスト
costs = media_data.sum(axis=0) # media_dataがimpの(imp / 1000) * CPMなどと変換するが今回はそのまま
# 売上データ
target = np.dstack((df_A.iloc[:,-1].values, df_B.iloc[:,-1].values)).reshape(113, 2)
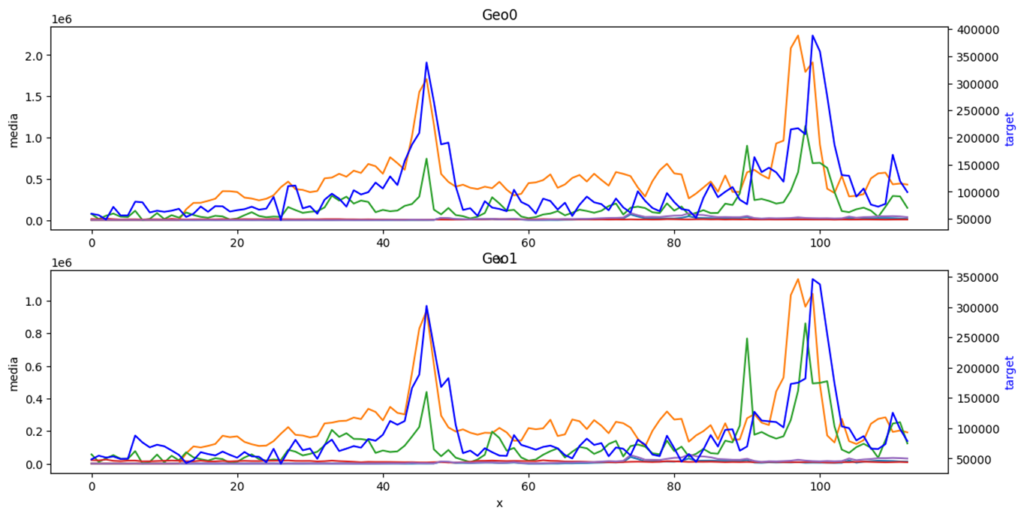
(参考) 使用するデータを眺めてみます。地域AがGeo0でJがGeo1。人工的に作成したデータのため地域差がないのはご容赦ください。
②-3 学習・検証分割
# Split and scale data.
split_point = target.shape[0] - 13
# Media data
media_data_train = media_data[:split_point, ...]
media_data_test = media_data[split_point:, ...]
# Extra features
extra_features_train = extra_features[:split_point, ...]
extra_features_test = extra_features[split_point:, ...]
# Target
target_train = target[:split_point]
②-4 スケーリング
media_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
extra_features_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
target_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
cost_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean, multiply_by=0.15)
media_data_train = media_scaler.fit_transform(media_data_train)
extra_features_train = extra_features_scaler.fit_transform(extra_features_train)
target_train = target_scaler.fit_transform(target_train)
costs = cost_scaler.fit_transform(costs)
②-5 モデリング
mmm = lightweight_mmm.LightweightMMM(model_name="adstock")
number_warmup=1000
number_samples=1000
mmm.fit(
media=media_data_train,
media_prior=costs,
target=target_train,
extra_features=extra_features_train,
number_warmup=number_warmup,
number_samples=number_samples,
seasonality_frequency=52,# 日次データの場合365として以下の変数のコメントアウトをはずす
# weekday_seasonality=True,
seed=SEED)
②-6 推定量
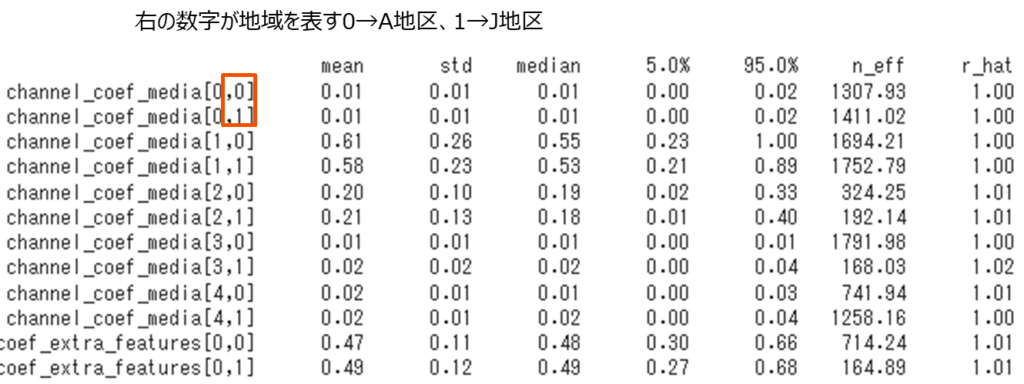
mmm.print_summary()
ただし、多いので一部のみ表示しています。
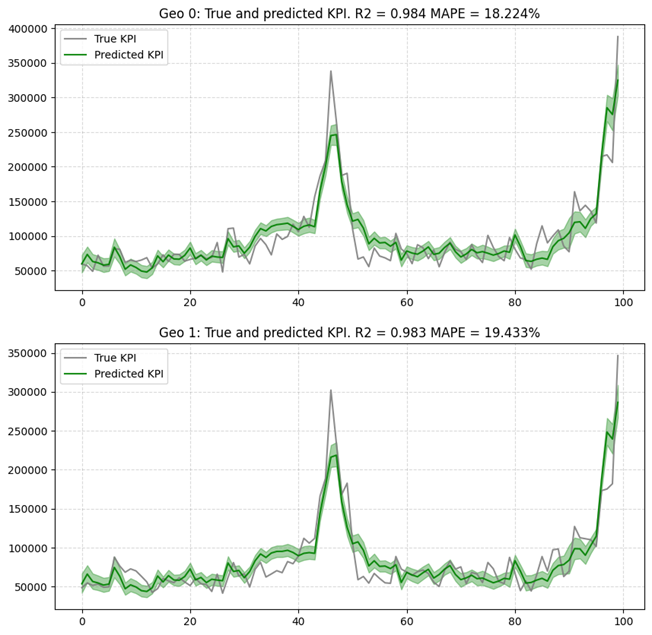
②-7 予実比較
# Here is another example where we can pass the target scaler if you want the plot to be in the "not scaled scale"
plot.plot_model_fit(mmm, target_scaler=target_scaler)
以降は、普通の場合と同じなので割愛します。
③ その他レポートのtips
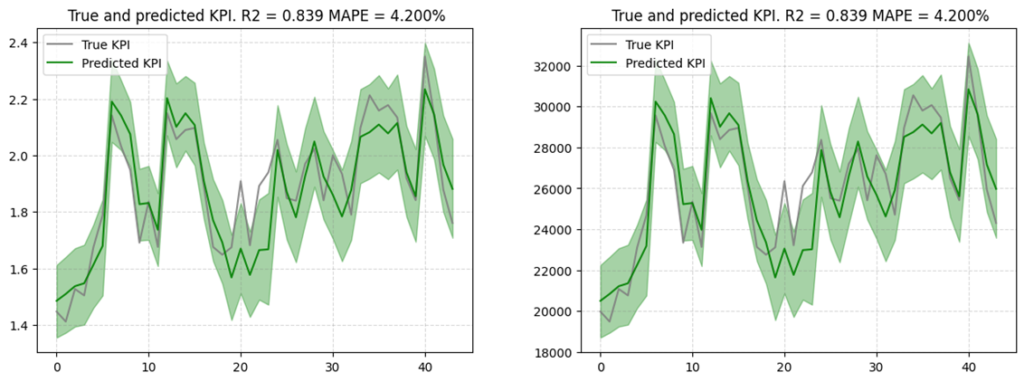
③-1 検証予測値を元の尺度で表示
lw3mのplotのデフォルトの軸の単位は標準化されているため、単位を元に戻して表示します。
# testデータに当てはめる
new_predictions = mmm.predict(media=media_scaler.transform(media_data_test),
# extra_features=extra_features_scaler.transform(extra_features_test),
seed=SEED)
# plotする
plot.plot_out_of_sample_model_fit(out_of_sample_predictions=target_scaler.inverse_transform(new_predictions),# target_scaler.inverse_transformで元の尺度に戻す
out_of_sample_target=target_test)
右下図がスケールを元に戻したものです。
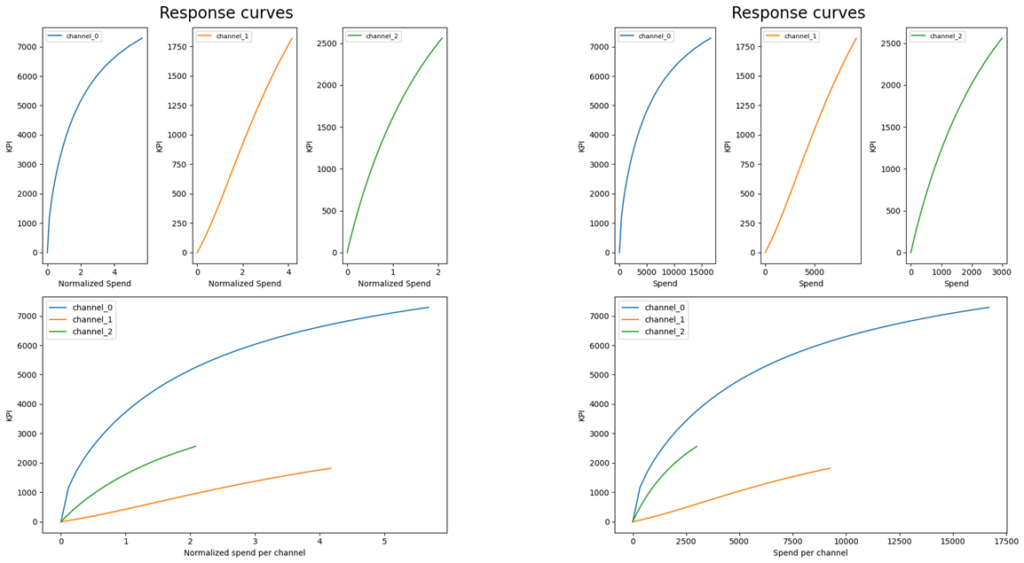
③-2 レスポンスカーブの横軸を元の尺度で表示
デフォルトでは横軸(メディア投下量)の尺度が標準化されているため、メディア間を同じように比較することができません。レスポンスカーブを元の尺度に変更する必要があります。
# メディア投下量と売上の関係
plot.plot_response_curves(
media_mix_model=mmm, target_scaler=target_scaler, media_scaler=media_scaler ,seed=SEED)
右下図が尺度を元に戻したものです。
④ 留意点
その他MMMを実行するうえでの留意点などに触れます。
④-1 各メディアの出稿の相関が強い場合
TVとネット広告を同じようなパターンで出稿場合(つまり共に分散が大きい)、成果への影響がTVかネットのものなのか判断できません。
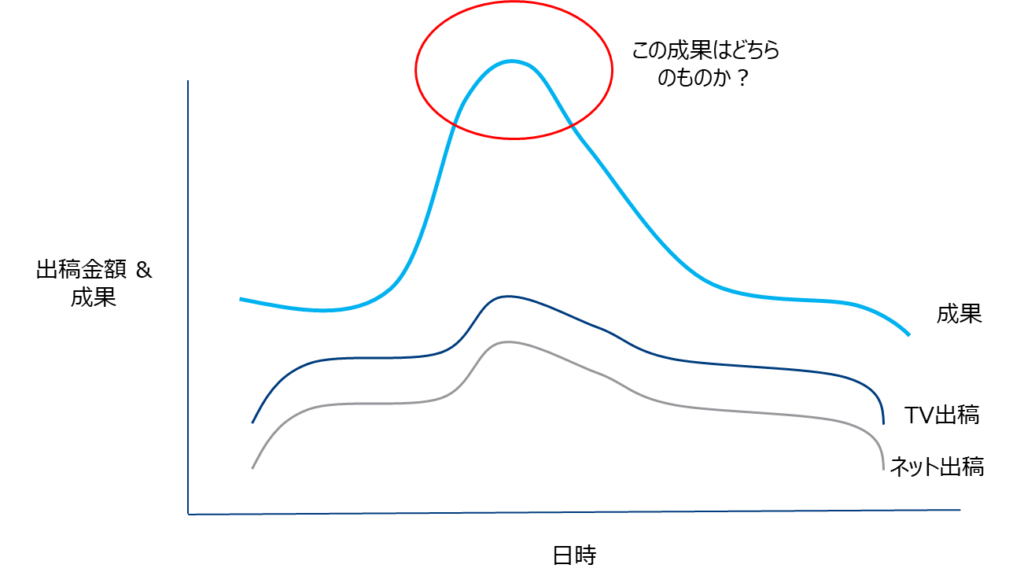
出稿パターンを計画的に行うなどして適切なデータを取得することが重要です。
これで落穂ひろい完了!
本当は見せかけの回帰についても述べたかったのですが、ベイズフレームワークでも最小二乗法と同じこの問題が生じるか調査中で、今回は触れませんでした。
何卒宜しくお願い致します。
無料相談大歓迎です。ご興味ございましたら、お問い合わせはこちらから宜しくお願い致します。

