前々回の記事で主成分の数理的な意味について解説しました。
今回はマーケティング実務を念頭においた、実践よりの解説をしたいと思います。
主成分分析概要
主成分分析は情報集約の技術であり教師なし学習に分類されます。連続数値変数を対象とした手法です。類似した手法にコレスポンデンス分析というものがありますが、これはカテゴリ(質的)変数を対象として主成分分析と見なせます。本節では主成分分析の特徴をコレスポンデンス分析と比較しながら紹介します。
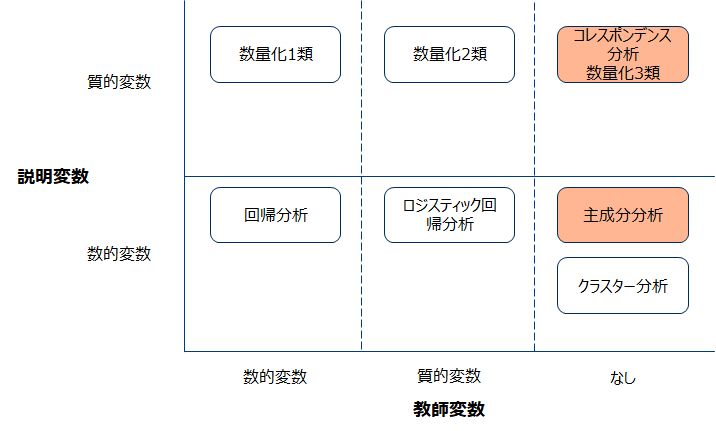
ユースケース
主成分分析は相関の強い変数を合成し低次元に要約した特徴量を作成することができます。例えば購買した品目からラグジュアリー志向、実用品志向などの特徴量を作成するなどです。

特に2次元の特徴量に情報を集約できた場合散布図を用いて可視化できるためマーケターにとっては有効な武器になります。
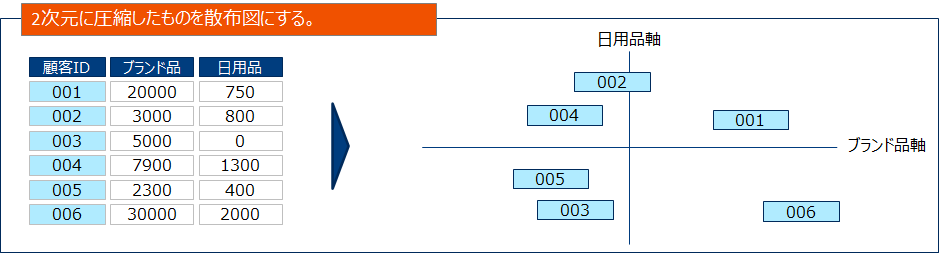
主成分分析は数値変数を対象とした手法でした。一方コレスポンデンス分析は質的変数データに対して適用可能ですので、実務上は以下のようなクロス集計表を要約する場合に使用することがあります。
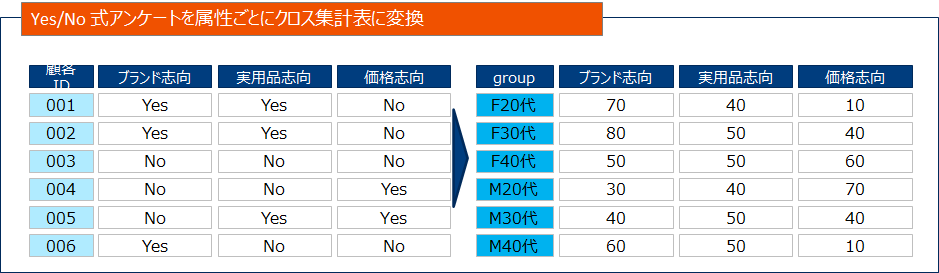
主成分分析と同様に、2次元の散布図を用いて可視化することができます。ブランドに関するイメージとブランドを2次元に配置し、他社ブランドと自社ブランドの関係図示することでマーケティング戦略に活かすような使い方ができます。
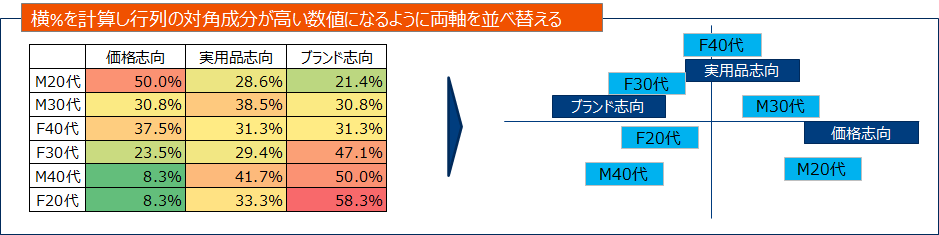
主成分分析の活用
本論に入る前に改めて主成分分析のイメージを復習しましょう。
イメージ
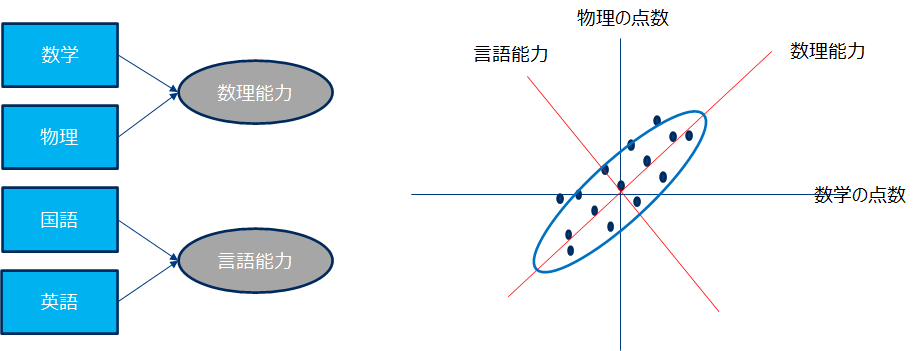
例えば定期テストの「数学」「物理」の点数は相関があると考えられ、同様に「国語」「英語」にも同様な関係があると考えられます。前者を数理能力、後者を言語能力として得点化することで4つの科目の点数を2つの量に変換できます。下右図を見ると数学と物理は相関が強いため散布図がラグビーボールのように楕円形です。この長軸方向の成分を数理能力とします。
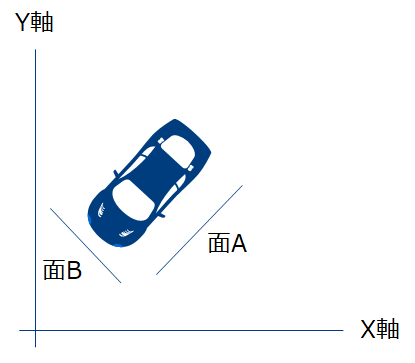
もう一つ具体的なイメージを紹介します。以下の図は上から車を見た図です。1枚だけ車の情報がなるべく多く含まれるように写真を撮影する場合、どこから撮影するのが適切でしょうか?
解答) 面Aに平行な面(すなわち横面)から撮ればよい。
もう一枚追加で撮影できる場合どこから撮影するのが適切かでしょうか?一枚目とは異なる情報を多く含むようにしたい。
解答) 先ほどの面Aと垂直な面B(すなわち車の正面)から撮れば良い。
面A方向を第1主成分方向、面B方向を第2主成分方向と呼びます。
マーケティングへの活用 ~多変量データの要約~
冒頭でも活用のユースケースを紹介しましたが、マーケティングへの活用案をもう少し具体的に説明してみます。一般的にマーケティングで使用するデータは多変量(高次元)であるため解釈は困難です。そのため主成分分析で2次元に要約することで可視化を行います。
アンケートデータの要約
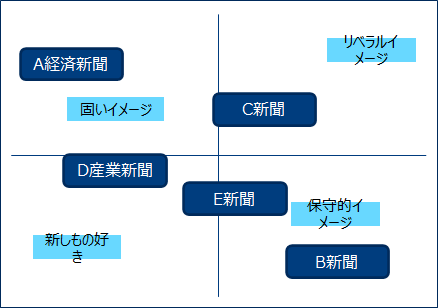
ブランドのイメージに対してのアンケートデータを要約します。
自社ブランドと他社ブランドのポジショニングマップを作成し、次なる戦略を練ります。または空いているポジションに新規ブランドの検討をします。
アクセスや購買トランザクションデータの要約
トランザクションデデータを要約し、自社顧客のグルーピング及び可視化を行います。具体的には得られた主成分を用いてクラスタリングして、2次元のマップに可視化します。

実行手順
ここからは実際にpython上でコードを実行し手順を確認しています。コードの実行方法は
- https://github.com/mitsu666/DataScienceLecture/blob/master/01_PrincpalComponentAnalysis_wine.ipynb からファイルをDLします。
- DLしたファイルをご自身のgoogle driveに置きます。
- Google drive上から開くと、 Google colaboratoryに遷移します。そこで実行できます。
実行手順概要図
以下は大まかな手順の概要です。右のアルファベットは対応するpgmの箇所を示しています。

データ準備
主成分分析を実行するために以下を満たすデータが必要があります。
- 欠損がないこと。
- 全て数値であること。(整数もOK)
- 一つのIDが一行に対応していること。(例えば購買データであれば顧客ID1つがデータ1行に対応)
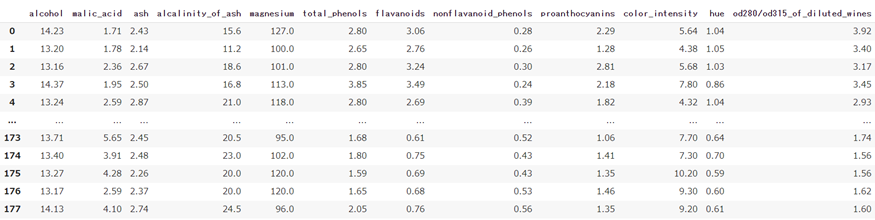
今回pgm内で用いるデータセットはschikit-learnに含まれているサンプルデータセット(wine)です。これは全て数値データであり欠損がないため特別な処理は不要です。
主成分分析実行
主成分分析を実行するためには専用ソルバーを用います。RやPythonでは対応したオープンソースのライブラリとして専用ソルバーが用意されており、またSAS/SPSSのような有償ソフトウェアにも同様の機能があります。pgm内ではPythonで行うためsklearnのライブラリを使用します。
| ソフトウェア | ライブラリ/プロシージャ |
|---|---|
| Python | sklearn decompositionパッケージのPCAライブラリ |
| R | Stats パッケージのPrincompライブラリ |
| SAS | proc princomp |
| SPSS | Modeler 標準で搭載 |
異なるアルゴリズムで実装されているライブラリがありますが、これは相関係数行列(すなわち標準化後データ)を用いているか分散共分散行列(標準化前データ)を用いているのかの違いです。
計算方法は実にシンプルであり、相関係数行列(分散共分散行列)の固有値問題を解いているだけです。相関係数行列は対称行列であるため、必ず次元と同じだけの実数固有値を持ちます。
主成分得点・係数/因子負荷量/寄与度の確認
主成分分析に登場する言葉を確認しておこう。
主成分得点・係数
各変数に対応した重み係数をかけて足し合わせたものが主成分得点です。a1i(i=1,..n)の絶対値が大きい(小さい)場合主成分得点との相関が強い(弱い)変数です。係数はソルバーがが算出してくれるので、算出方法を覚える必要はありません。

因子負荷量
主成分得点とある変数の相関係数を因子負荷量と呼びます。上記の係数が主成分方向のみの情報しか持たないことに対して、その主成分得点への影響度合いを情報として持ちます。
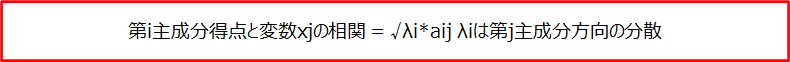
寄与度
第1主成分、第2主成分、第i主成分…第n主成分の順に元の変数の情報を多く保有します。第i主成分が保有する情報量を寄与度,第1主成分から第i主成分までの累積の情報量を累積寄与度と呼びます。一般的に第i主成分までの累積寄与度が80%を超えていればi個の変数で元の変数を良く説明できていると考えます。
寄与度はソルバーが算出してくれるので、算出方法をを覚える必要はありません。

寄与度のイメージは以下をご参照ください。

2変量の相関が強いほど、楕円の扁平率は大きく、つまりより尖ったラグビーボールのようになります。そのため赤い線はほぼ0となり寄与度は100%に近づきます。
実際にpgmを実行し因子負荷量を確認します。Prolineは尺度が異なっているため係数では他より極めて大きくその他の変数の寄与は見られませんでした。一方因子負荷量では他の変数が主成分得点に寄与していることが分かります。
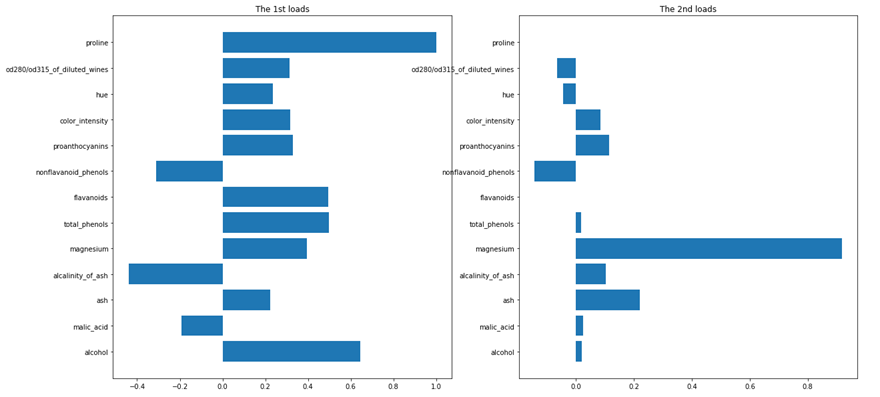
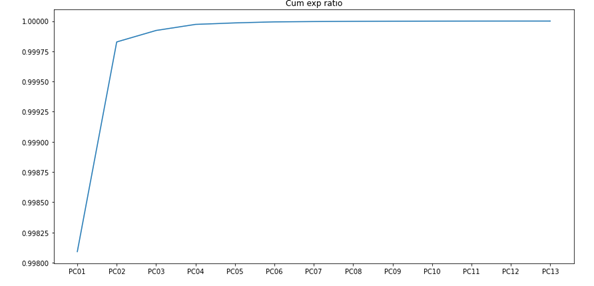
寄与度を確認すると、上位2つの変数で寄与度は99.75%を占めています。この結果から13変数を2変数に圧縮してもよさそうであることが分かります。
プロット
2次元に要約できたので、これを散布図に落とします。
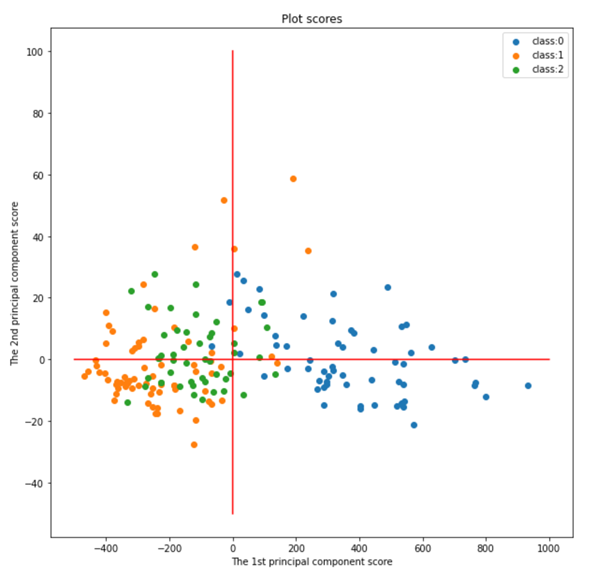
同一のワインのクラスは近い場所に異なるものは遠い場所にプロットできています。さらにここから元の変数の情報を加えてより精緻な散布図を作成します。
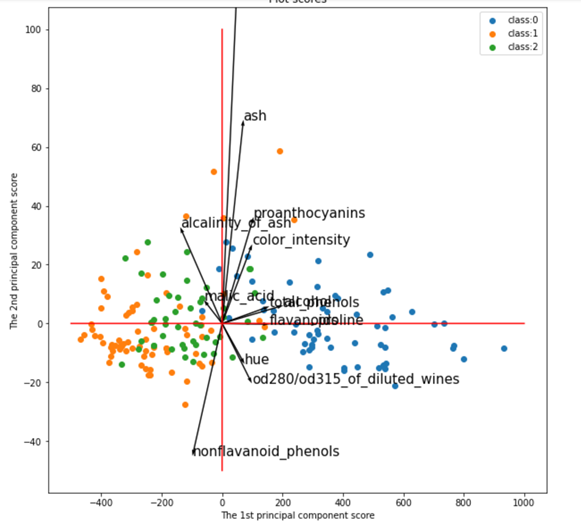
上記の図はマーケティング分野でブランドマップと言われるものに応用されています。

