先月末にデータ解析や機械学習の前処理に関する本を共著させて頂きました。(本については右側サイドバーにリンクがあります)私はテーブルデータの前処理に関する内容(chapter2)を執筆しました。その中の次元削減の章で主成分分析の説明をしている箇所があります。そこの元の原稿では主成分分析の数理的な説明をしている箇所があったのですが、前処理という本のコンセプト上お蔵入りしてしまいました。従って今回の記事はそのお蔵入り原稿を元に主成分分析の数理的意味を考察したいと思います。
主成分分析のモチベーション
多変量データには互いに相関の強い変数がある場合があります。例えば数学と物理の点数、や人口密度と地価などです。これら相関の強い変数は非常に似ているため両方使用するよりまとめたほうが計算量的にもリーズナブルですし、また10変数くらいを2変数にすることができれば散布図で多変量データを可視化することができます。先ほどの例ですと数学と物理の変数を合成して例えば「理科系能力」、人口密度と地価を合成することで「都市化指数」と定義できるかもしれません。
主成分分析の考え方
以下は上空から車を見た図です。もっとも車体が大きく写る面から写真を取りたいと思った場合面Cから取るのがよさそうです。見れば明らかなのです一番車体の全体像を捉える事ができています。X軸,Y軸に並行な2面から2枚写真を取るよりC面からとれば一枚で済みそうです。主成分分析はこのようにX,Y軸に平行な面から2枚写真を取る代わりに1枚だけ取っていい場合最も効果的な面を探す手続きなのです。
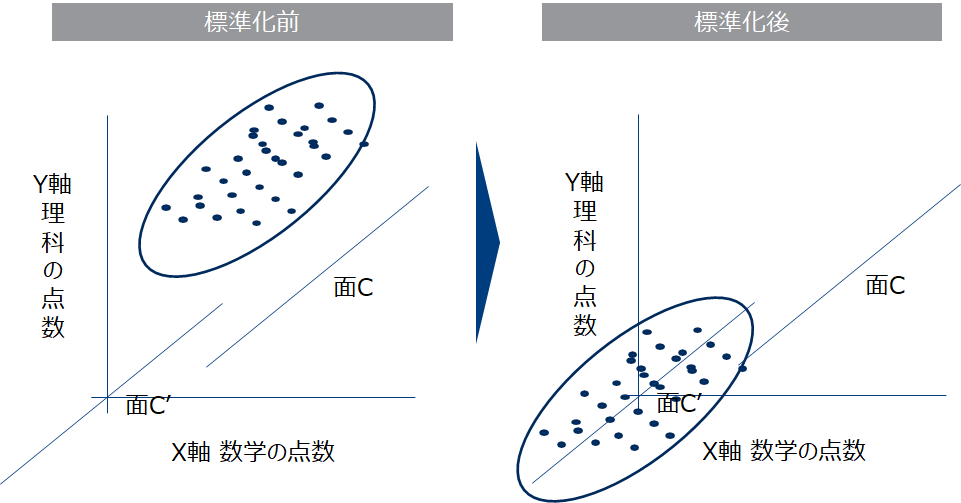
数学と理科の点数は相関が高いため以下のような散布図になると予想されます。このとき上の自動車の例と同じように2つの変数が作り出す楕円のラグビーボールの全体像が捉えられる面Cに新たな合成変数を作成すると元の情報(全体像)の損失を最小にしたまま次元を2→1にできます。面Cは2次元ユークリッド空間上のベクトルなので平行移動しても議論は変わらないのですが、今はX軸Y軸の交点を0ベクトル(原点)とするベクトル空間を考えるため面C’を伸ばした直線が原点を通るように記述しておきます。(こうすることで面Cは部分空間となります)また数学、理科の点数を標準化(平均0、標準偏差1)すると下左図のように楕円の中心を面C’が通るようになります。
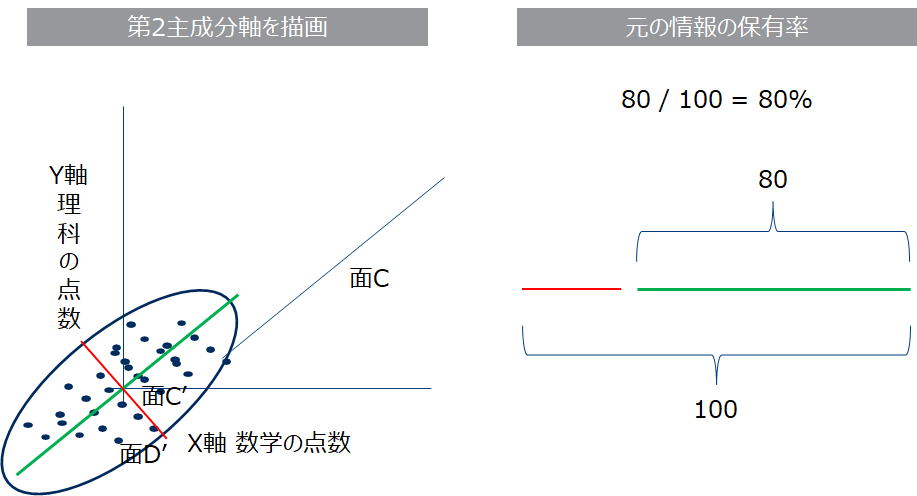
ところで面C’だけで元のデータの情報量をどれだけ説明できているのという問題が残ります。ここでもう一枚だけ面C’以外から写真を取っていいとすると面C’では捉え切れえなかった部分を取る方がよさそうです。答えを言ってしまえば面C’に対して垂直な面D’(赤い線)から取ると面C’で補足できなかった情報を得る事ができます。この赤い線と緑の線を足したものが元の情報全体で、それに対して緑の線の長さが1次元に削減した場合の元のデータの情報保有率です。緑の線を第1主成分、赤の線を第2主成分、元のデータの情報保有率を寄与率と呼びます。一般的に寄与率が80%以上あれば「良い次元削減」と言われています。
数学的定式化
上記第1主成分。第2主成分を数学的に定式化します。元のデータを(x,y)とします。2次元ベクトルa1 = (a11,a12) ,a2 = (a21,a22)を用いて
z1 = a11*x + a12*y
z2 = a21*x + a22*y
とするとz1,z2は(x,y)座標をある面に射影したものになります。次にz1,z2はラグビーボールの長半径、短半径と重なるようにa1,a2を選びます。これを選ぶにはz1の分散を最大に、z2がz1に直行するように選ぶ事で実現できます。
上記定式化の元でa1,a2を求めることが主成分分析のアルゴリズムの根幹になります。
主成分分析アルゴリズム
これを読んでいる賢明な読者はご存知の方もいると思いますが、主成分分析は与えられたデータの相関係数行列の固有値問題であるというのを聞いた事があると思います。一方でこれは本質を少し見えにくくしています。固有値問題であることが本質ではなく、分散の最大値問題を解くと結果として固有値問題の式が残るというのが正しいです。
では計算を行って行きます。2次元の場合を考えます。
①まず主成分分析のモデルはZ=AXと行列とベクトルを用いて記述され、Xは標準化された特徴量ベクトルとします。
②第一主成分をこのZの1行目とすると、その標本分散は 1/(n-1)Σ(a11*x+a12*y)^(2)です。
③これを変形すると、a11^2+a12^2+2a11*a12*r12となります(但しr12はx,yの相関係数)。
④これを最大化するのですが、a11,a12に何の制約もない状態ですと、どこまでも大きくできるのでa11^2+a12^2=1とします。
⑤制約付き最大値問題を解くにはラグランジュの未定乗数法を使います。式を変形しa11,a12で偏微分を行い=0とした式を整理するとX^tXa=λa(左辺は相関係数行列、λはラグランジュの未定乗数法の乗数となります。)となります。
この式をよく見てみましょう。これは相関係数行列の固有値λと対応する固有ベクトルaが解であることを表しています。相関係数行列は対称行列ですので固有値は実数であり、その数はここでは2個です。それを大きい順にλ1>=λ2とした時固有値λ1に対応する固有ベクトルa1が第一主成分の主成分負荷量となります。式の両辺にこのa1をかけると対応するλ1はz1の分散になっていることがわかります(初学者が情報量=分散=固有値でつまづくのは固有値の数学的な意味の解釈の難しさにあります)。このように主成分分析は数学的には相関係数行列の固有値問題として捉えることができるわけです。仮にx,yが標準化されていない場合相関係数行列は分散共分散行列となり、同様に固有値問題の解として主成分負荷量が導かれます。
相関係数行列の固有値問題と主成分分析
先ほど数学的定式化の計算結果として固有値問題が出てくると申しました。しかしもう少し相関係数行列の固有値問題が意味することを考察してみます。
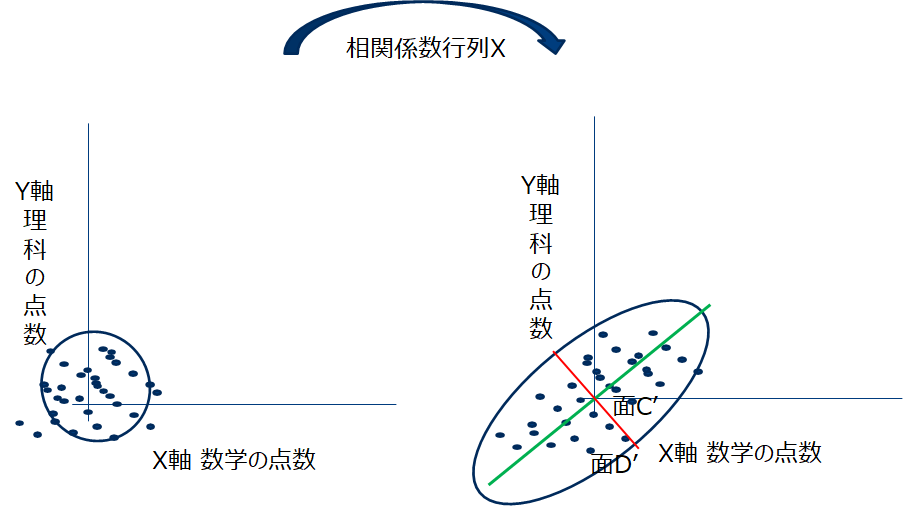
相関係数行列は対称行列であるためその線形変換は回転しません、また先の計算の途中で見たようにその固有ベクトルはラグビーボールの長半径、短半径方向でした。従って相関係数行列の引き起こす線形変換は、独立に分布する2変数をその相関係数行列が規定する相関関係を持つ2変数に変換するものと考えられます。これはキレイな単位円を楕円に引き延ばす変換として捉えることができ、その固有ベクトルの方向は楕円の長半径、短半径方向で固有値の大きさは引き延ばす強さと考える事ができます。
参考文献
多変量解析入門「永田」
データ解析の実際 多次元尺度構成法・因子分析・回帰分析 「奥、高橋」

