前回の続きをやっていきましょう。今回はPearl流のバックドア基準とRubin流の傾向スコアをご紹介します。
バックドア基準
交絡因子を定義
因子(例えば性別)が介入有無(例えばCP対象か否か)、反応(例えば購買したかどうか)双方に影響を与えている場合、その因子を交絡因子と呼びます。その場合介入効果を計測するためには、因子の層ごとに(例えば因子が性別とすれば、男性/女性それぞれ)クロス集計を行う必要があることを前節で述べました。この節では今まで直観的な理解にとどめていた交絡因子に対して厳密な定義を与えます。
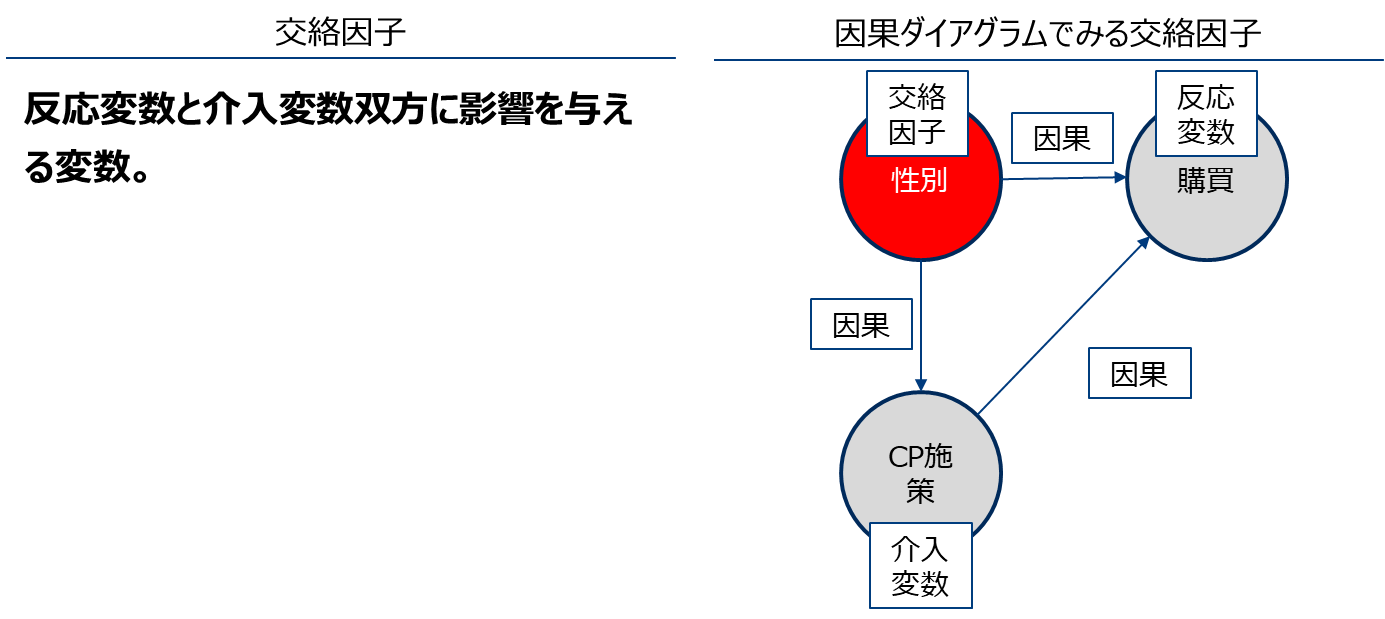
交絡因子である場合/ない場合、または複数ある例
様々な因果ダイアグラムが考えらえれます。交絡がない場合は簡単ですが、複数ある場合が問題になります。
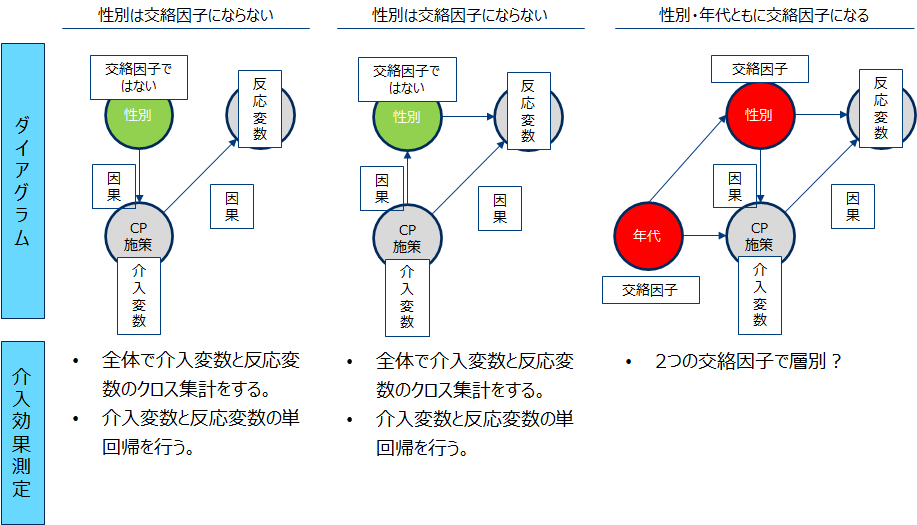
必要な交絡因子のみで調整する
実は上記3番目の例では性別だけで調整(層別)するだけで、介入効果は測定できるのです。これは性別で層別すると値が固定され、年代変数が反応変数へ与える影響がなくなるからです。
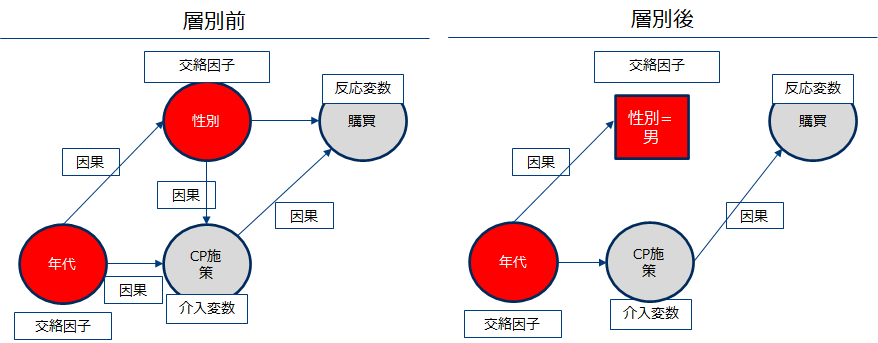
層別にすべき変数集合の十分条件
先の例では変数が2つであったため層別すべきの変数の特定は比較的わかりやすかったと思います。しかしより一般的な場合であっても同様に層別すべき変数集合を特定したいというのが人情です。この特定のための十分条件としてバックドア基準が考えられました。バックドア基準を満たす変数集合で層別することで調整した介入効果を計測できます。

バックドア基準を満たす変数集合は複数存在する
同じ因果ダイアグラムにおいて、バックドア基準を満たす変数集合は複数あります。以下の図において、{性別}のみからなる変数集合、{年代,性別}の複数の変数からなる変数集合はバックドア基準を満たします。一方{年代}はバックドア基準を満たさないことに注意します。
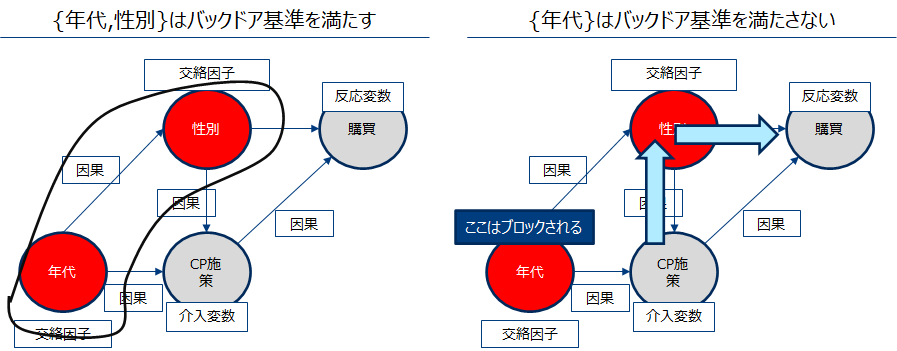
変数選択
バックドア基準を満たす変数集合を説明変数として重回帰した場合、介入効果xの偏回帰係数は介入効果の総合効果(間接効果+直接効果)となることが知られています。そのためバックドア基準を満たす変数集合の中で最小のサイズの変数集合を重回帰モデルに投入することで最小の情報で、介入効果を計測できます。例えば以下のような因果ダイアグラムがある場合「性別」以外の交絡因子を無視して介入効果の測定ができるということです。

傾向スコア
調整交絡因子が多い場合に層別するのは大変
以下のような因果ダイアグラムが得られたとき、調整する交絡因子が多いため層別する層数も大きくなります。
ただし、{年齢,性別,職業}の変数集合はバックドア基準を満たしていることに注意します。
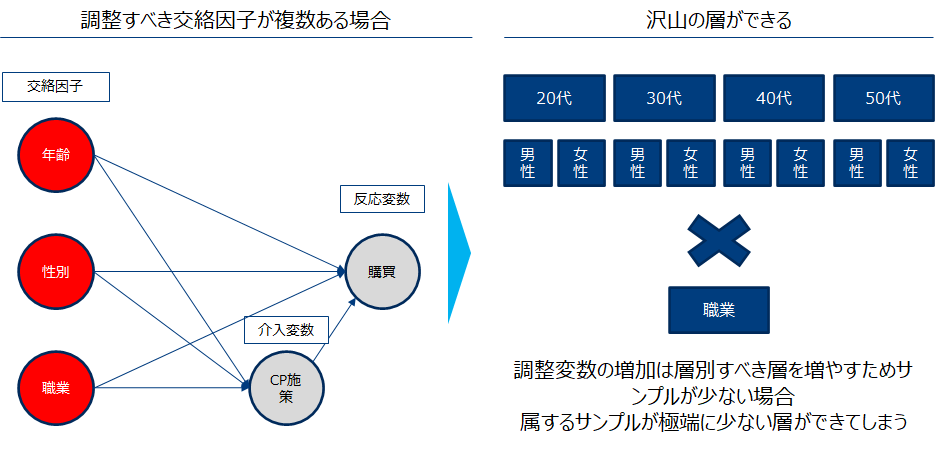
多次元層別変数を1次元に圧縮したい
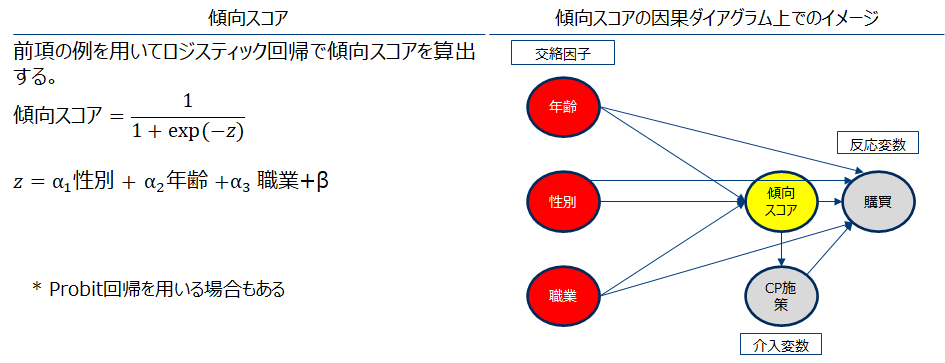
調整すべき因果が多い場合、それらを圧縮したスコアを算出して次元を削減したいと考えます。スコアのアイデアとして調整交絡因子が与えられたもとで介入を行う確率を考えます。実務的には目的変数を介入有無(有=1,無=0)、説明変数を交絡因子としたロジスティック回帰を実行する事で算出すします(Probit回帰を用いる場合もあり)。このように算出されたスコアを傾向スコアと言います。
右下図は傾向スコアを因果ダイアグラム内に記述した場合のイメージです。{傾向スコア}は単独でバックドア基準を満たすため、複数変数での層別が不要になります。
例題
左下図のような因果ダイアグラムから生成されたデータが得られた時、この時のCP施策の効果を知りたいとします。{年齢,性別}はバックドア基準を満たすため、これらを用いて傾向スコアを算出することを考えます。
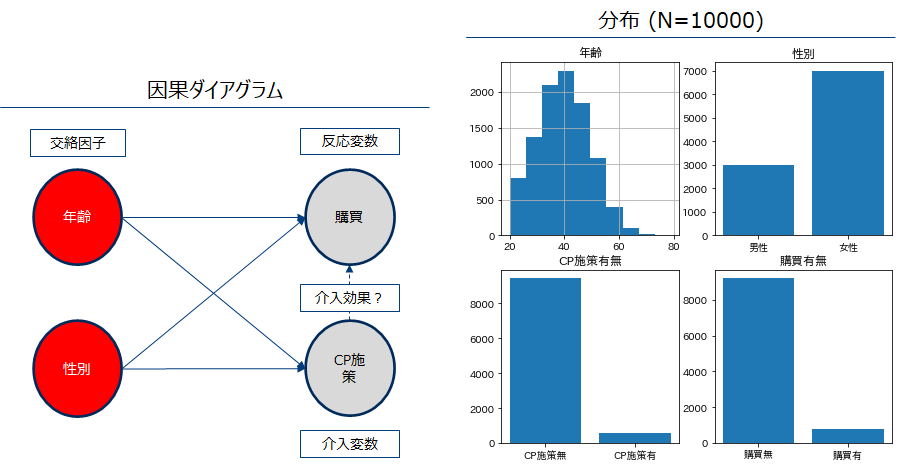
全体のクロス集計結果を見ると、介入が購買影響したと考えられます。この結果からCP施策は有効であったと結論づけられるでしょうか?
No→前項因果ダイアグラムより性別や年齢は交絡因子であるため調整する必要があります。

算出された傾向スコアを0.02間隔で層別しました。いずれの層でもCP施策有無それぞれの集団ごとの共変量の平均はほぼ同じになりました。(つまり傾向スコアでの層別は共変量の影響を調整している)
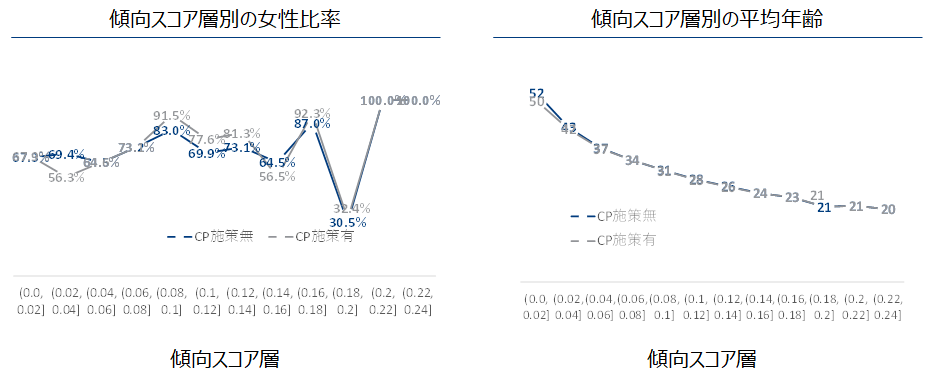
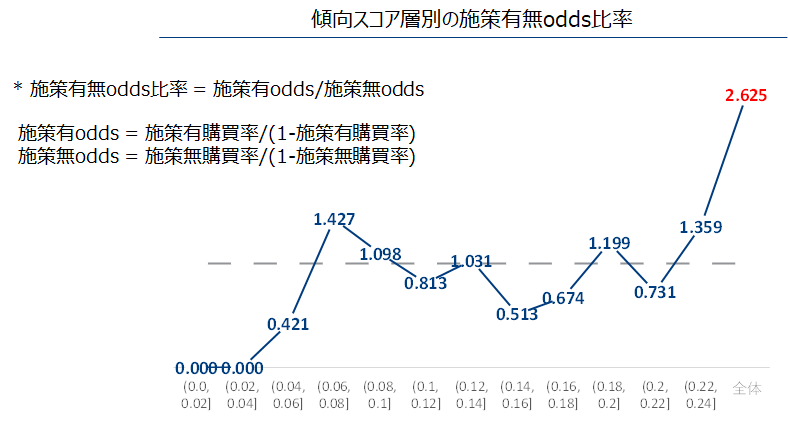
傾向スコアの層別と集団全体に対して施策有無ごとの購買率のodds比率を計算しました。全体でのodds比率は介入効果があったことを示唆している(前項全体クロス集計の結果と同じ)一方、層別でみるとodds比率は1の周辺を分布していることから介入効果があるとは言えないのです。
まとめ
因果推論と交絡因子の調整
- 因果推論はある介入(CP施策など)の応答(売上など)への効果を測定するために行う。
- しかし介入と応答が他の変数に影響を受ける場合(女性に対して優先的にCP施策を行う)、それら影響を与える変数を調整したうえで効果を検証する必要がある。(このような因子を交絡因子と呼ぶ)
- 交絡因子の調整は層別や重回帰にそれらを投入する事で行う。
因果ダイアグラムとバックドア基準
- 調整変数の特定には因果ダイアグラムを作成し、バックドア基準を満たすかどうかを調べる必要がある
- バックドア基準を満たす変数集合で層別することで、介入効果を正しく計測できる。またそれらを説明変数とした場合の介入効果の偏回帰係数=介入の総合効果となることが知られている。
傾向スコア
- 調整変数が多い場合傾向スコアを用いることで、調整可能である。

