施策の検証とA/Bテスト
マーケティングにおいて施策は販促の一種であるキャンペーンと、オペレーションやチャネルの改善のために行う改善施策に大別できます。

A/Bテストは施策や改善案を素早く検証することに適しています。特にオンラインコンテンツ(LPやwebUI)は小さな改善を繰り返すことで大きな効果を期待できるため、A/Bテストが果たす役割は大きいです。

事例
A/Bテストはビジネスのみならず選挙戦でも駆使されており、一定の成果をあげています。
- Bing(*1):Bingの検索結果の広告見出しの表示方法をテスト。とても小さいアイデアであり有効性に疑義があったが、簡単なA/Bテストで有効性が検証できたために、実装。ユーザ体験を損なうことなく、年間1億ドルの売上増加に繋がった。
- オバマ陣営(*2):2012年米大統領選においてオバマ陣営のデジタルチームに所属していたKyle Rush(*3)は、キャンペーンページに対して500回ものA/Bテストを行った。その結果6億9千万ドルの寄付金を集めた。この額は全体の寄付金の約7割を占めた。
(*1) A/Bテストの効果的な実施法 DIAMOND ハーバード・ビジネス・レビュー論文
ダイヤモンド社 ロン・コハビィ [著]、ステファン・トムク [著]、DIAMONDハーバード・ビジネス・レビュー編集部 [編]
(*2) (https://medium.com/convertize/the-secret-behind-obamas-2012-election-success-a-b-testing-no-really-df672c248926)
(*3) 現在Maisonette のCTOとのこと…彼のLinkedinより
(参考)
1700年代、イギリス軍艦の船長は地中海で働く船員に壊血病が発病しないことを発見した。この船に乗っていた船員に柑橘類が配給されていたことから、彼は半分の船員にライムを与え(治療群)、もう半分の船員にはもう半分の乗組員(対照群)には通常の食事を続けさせた。その結果ライムを摂取した群とそうでない群の壊血病の発症率は大きな違いがあった。(しかし壊血病がビタミンC不足の結果であることはその当時は知られておらず、またライムにビタミンCが含まれていることも知られていなかった)その後柑橘類を定期的に摂取するようになり、今でも人気のある「ライム」という呼称が生まれた(*4)。
(*4) Rossi, Peter H, Lipsey, Mark W and Freeman, Howard E. Evaluation: A Systematic Approach. 7th. s.l. : Sage Publications, Inc, 2003. 0-7619-0894-3.
全体評価基準(OEC)
Overall Evaluation Criterion
A/Bテストの目的となる定量的な尺度であり、短期的に観測可能かつ企業の長期的ゴールにつながるような指標と定義されます。さらに指標が複数ある場合、その組み合わせ(例えば線形結合)などを用いる場合があります。 (*5,6)
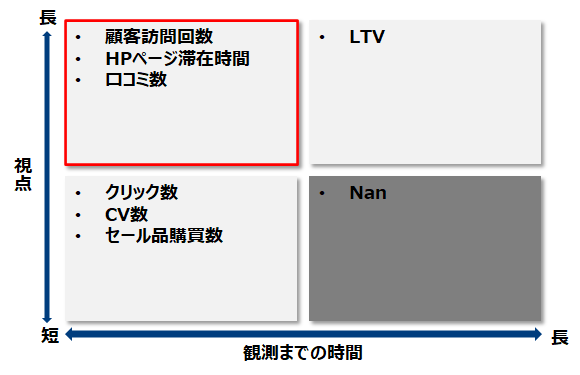
(*5) (https://daveredfern.com/overall-evaluation-criterion/)
(*6) Ron Kohavi et al., 2007 「Practical Guide to Controlled Experiments on the Web: Listen to Your Customers not to the HiPPO」
テスト
A/AテストとA/Bテスト
A/Bテストは何も施策をしないグループと、施策を行うグループにランダムに分けて実験をしその結果を比較します。一方A/Aテストは”施策を行わない”グループをランダムに分け同様な操作を行います。
- A/Aテスト:同一の属性を持つグループ同士を比較。テストの目的は「差がない」ことを確認する。主に(*7,8)ツールの正確性検証。成果指標のベンチマークを確認する。(検出力の見積もりにも使える)必要なサンプル数を見積もるため
- A/Bテスト:ランダムに分けれられた2群の片方を施策無(A群)、もう一方を施策有(B群)としてそれぞれの成果指標に「差があるかどうか」を確認する。
(*7) (https://vwo.com/blog/aa-test-before-ab-testing/)
(*8) (https://www.abtasty.com/blog/aa-test-waste-of-time-or-useful-best-practice)
A/Aテストは必要か
時と場合により賛否様々な意見があります。時間と予算とその効果を吟味してその有効性を検討する必要があります。

(*1) 「Why A/A Testing is a Waste of Time」 (https://cxl.com/blog/aa-testing-waste-time/)
(*2) (https://www.abtasty.com/blog/aa-test-waste-of-time-or-useful-best-practice/)
(*3) 「Running A/A Tests is a Waste of Time and Money」 (https://www.brooksbell.com/resource/blog/running-a-a-tests-is-a-waste-of-time-and-money/)
本稿のスタンスとしては時間もコストも係ることから、特に新規ツールを導入して複雑なことをやる場合を除いては不要と考えます。特にオフライン施策やキャンペーンの評価では時間やコストの問題からA/Aテストを行う同意をステークホルダーから得られない可能性が高いです。また本稿で最後にオススメするベイズ的手法ではここら辺多分あまり考慮しないで良いです。
A/B テスト工程

テスト設計 対象グループを選択
基本的にはランダムに同数のグループが2つできるようにします。しかしWebコンテンツの改善案検証とマーケティング施策の効果検証では少々やり方が異なります。
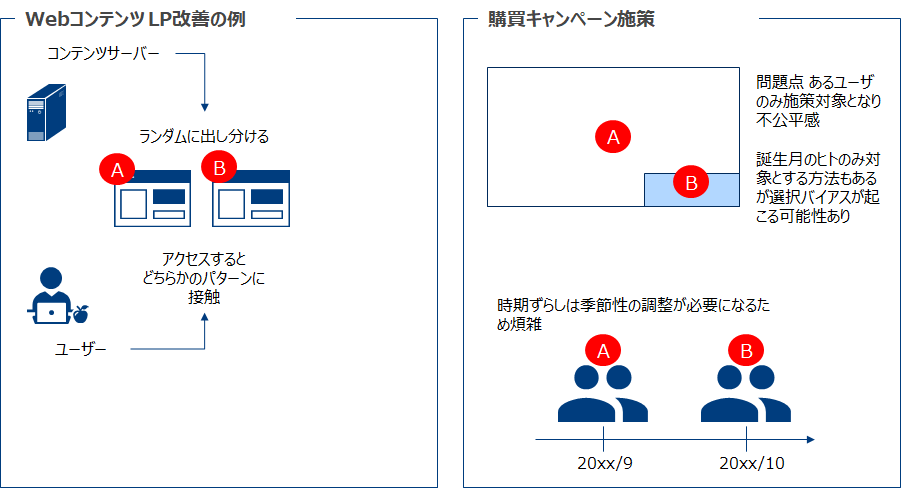
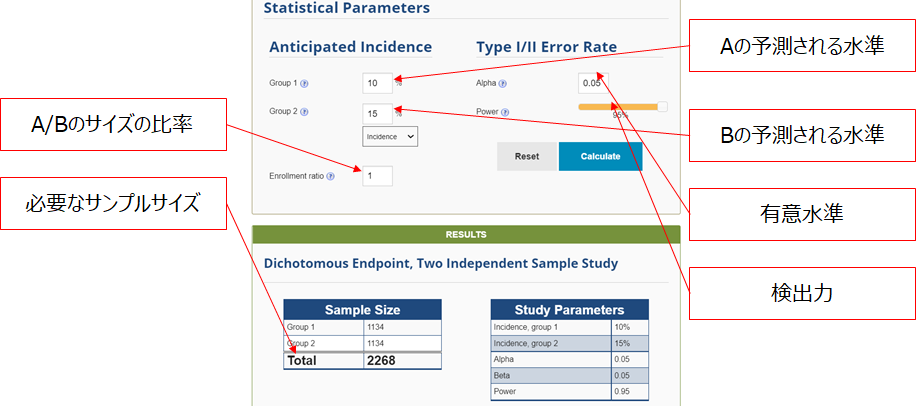
テスト設計 想定サンプルサイズの見積もり
サンプルサイズが小さい場合、A/Bの差が偶然のものなのか判断するのが難しい。そのため一定数のサンプルサイズを確保する必要があります。
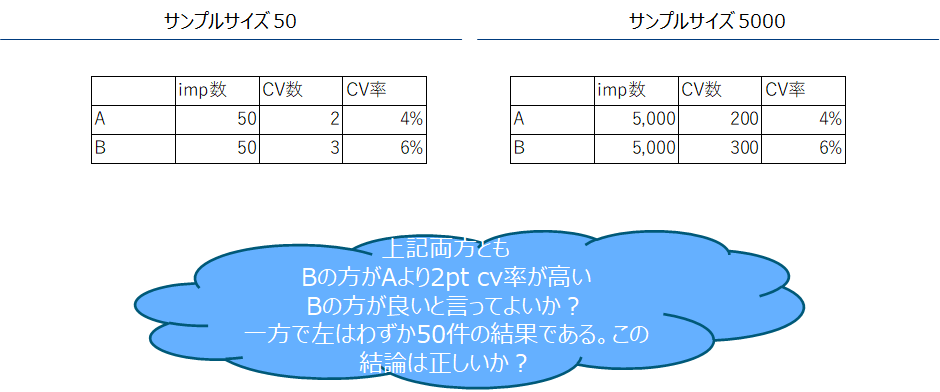
古典統計的仮説検定を(特に母比率の検定)行う前提である場合、「検出力」と「有意水準」、「想定する効果」の3つの要素でサンプルサイズを決めます。
- 検出力を決める。検出力は大きい方が良い(0.8~0.95程度)。
- A=Bという仮説が棄却される有意水準を決める。慣習的に5%とすることが多い。
- A=1%、B=2%のような期待されるAとBの差を決める。差が大きいと少量のサンプルで済むが現実的ではなくなる。
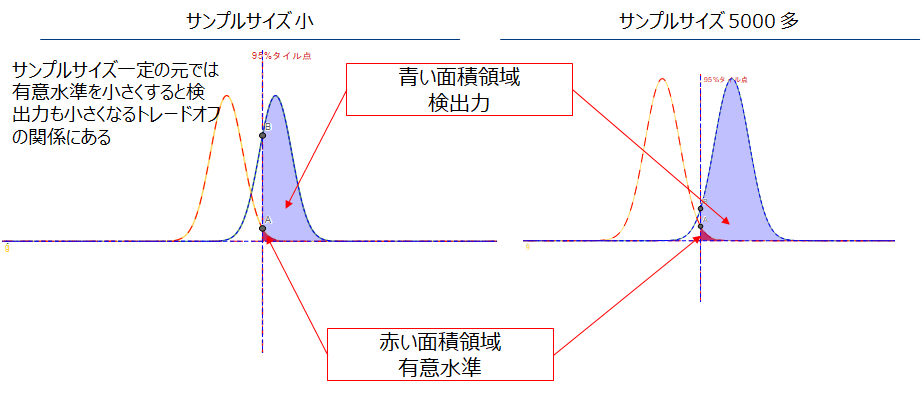
サンプルサイズの計算は大変煩雑であるが、以下のサイトで簡単に計算できます。
- Sample Size Calculator https://clincalc.com/stats/samplesize.aspx
- Evan‘s Awesome A/B Tools https://www.evanmiller.org/ab-testing/sample-size.html
A/Bテスト 評価
まず始めにクロス集計を行います、目検で異常な値でないかを確認し統計的な評価を行う。評価方法は古典的な統計的仮説検定またはベイズ的手法で行います。
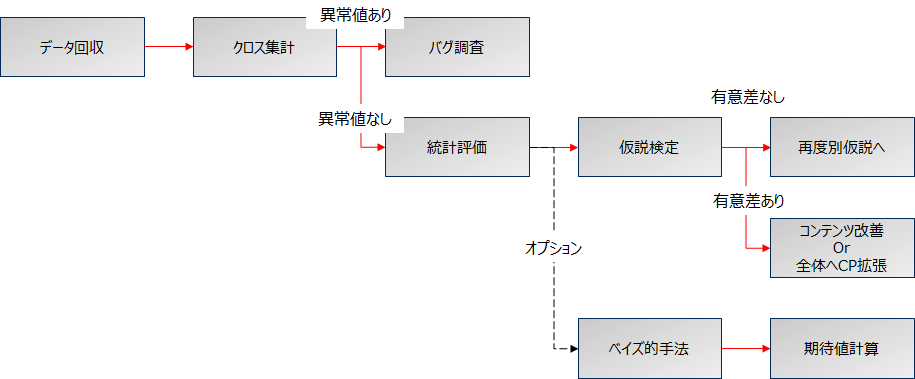
A/Bテスト 仮説検定
マーケティングの多くはAB間で、ある割合を比較することが多いです。例えば来館率や購買率、DM反応率などです。比率の検定のためには「母比率の検定」を行います。
[母比率の検定]
片側検定で有意水準5%の場合、右の式で定義される、Tが1.645より大きい場合に帰無仮説(A/Bの差がない、つまり施策は無意味であった)は棄却される(つまり仮説に意味があった)。
下の式のpA/pBやnA/nBはそれぞれA/Bテストのケースに対応、一般的にAがコントロール群(何もしない)Bが介入群(施策対象)である。
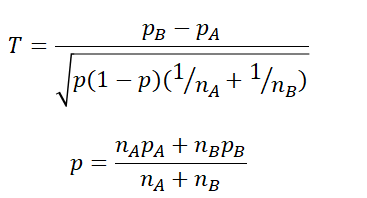
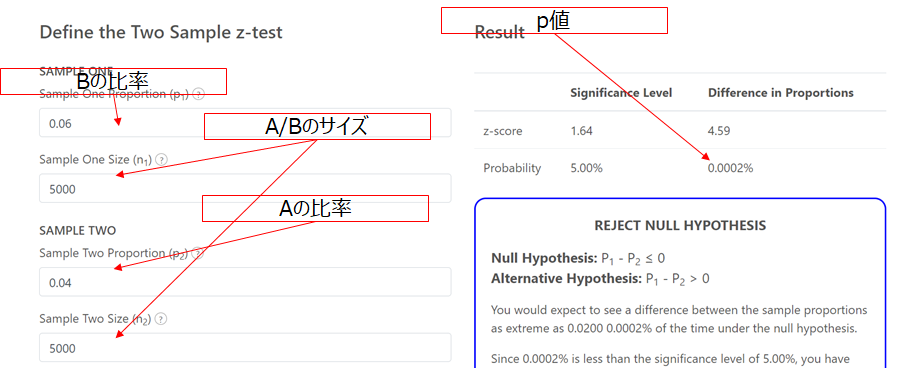
エクセルで計算した例が以下です。
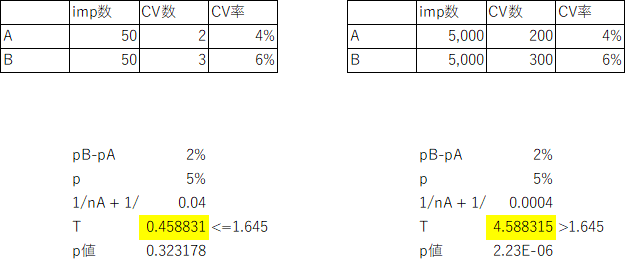
Web上で計算できるサービスもあります。
- https://www.infrrr.com/proportions/difference-in-proportions-hypothesis-test-calculator
- 上記サイトでは件数が170件程度ないと計算してくれない。
- またp1はB群に相当、p2はA群に相当するために逆にしてしまわないように注意する。
A/Bテスト ベイズ的アプローチ
仮説検定による評価にはいくつかの問題があります。
- 有意水準の数値に特に根拠がない。
- さらに5%とした場合平均して20回に1回は帰無仮説が正しい状況であってもこれを棄却してしまう。
このため多重比較を行う場合、有意水準を調整し検定を行います。(Bonferroni法、Holm法など)
一方でこれら手法とは異なる事前確率を用いて事後確率を計算するベイズ的手法が近年注目されています。A群/B群の母比率の確率分布を求める手法であり、施策が有効である”確率”そのものを算出することができます。

以下の結果からそれぞれの分布を求めてみます。
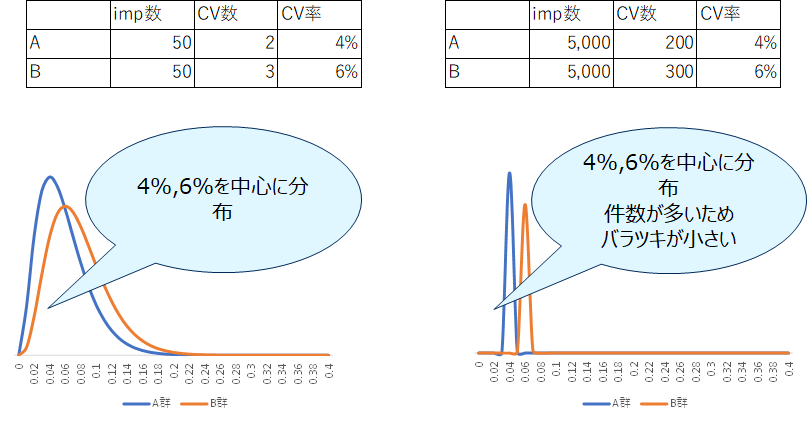
pB>pAの確率を求める。直接積分を計算をするのは大変なためサンプリングプログラムを書いてpB-pAの分布を求めます。
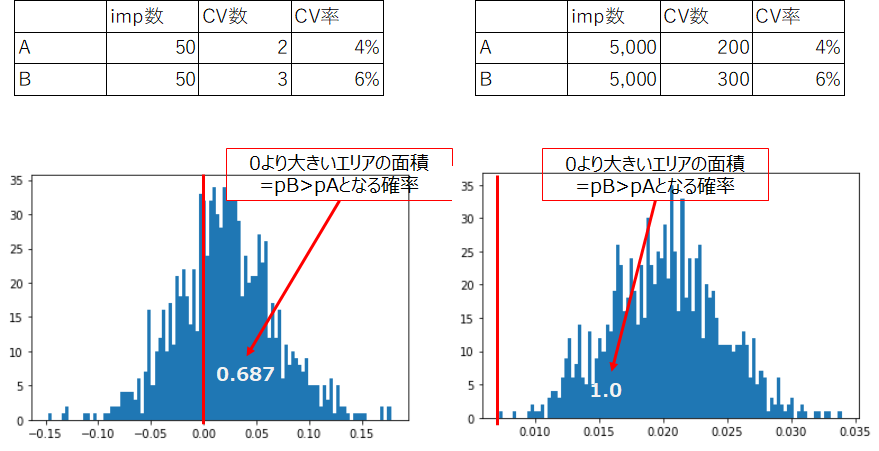
(参考)サンプリングプログラム
#baysiena A/B test import math from matplotlib import pyplot from scipy import stats import numpy as np import matplotlib.pyplot as plt snum = 1000 Na=50 na=2 Nb=50 nb=3 beta1=stats.beta(na+1,Na-na+1) beta2=stats.beta(nb+1,Nb-nb+1) p2 = beta2.rvs(snum) p1 = beta1.rvs(snum) print ((p2-p1>0).sum() / snum) plt.hist(p2-p1,bins=100)

