改めて前回の回帰モデルの俯瞰してみましょう。
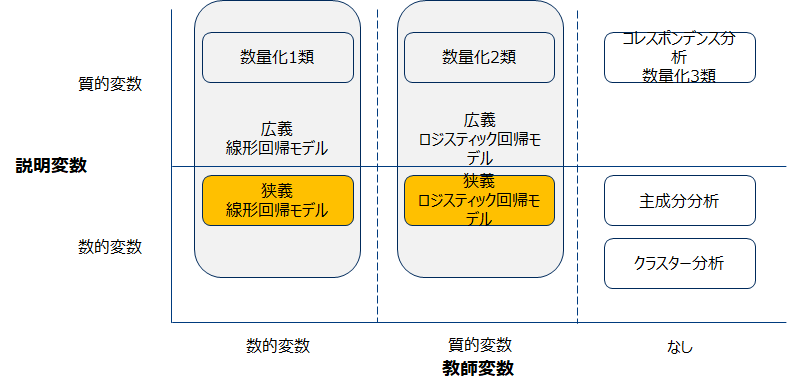
前回は数値変数を教師変数とする線形回帰について勉強しました。今回は教師データが質的データであるロジステイック回帰について実際のコードを追いながら実習します。
復習のため一般的なプロセスを再掲しておきます。
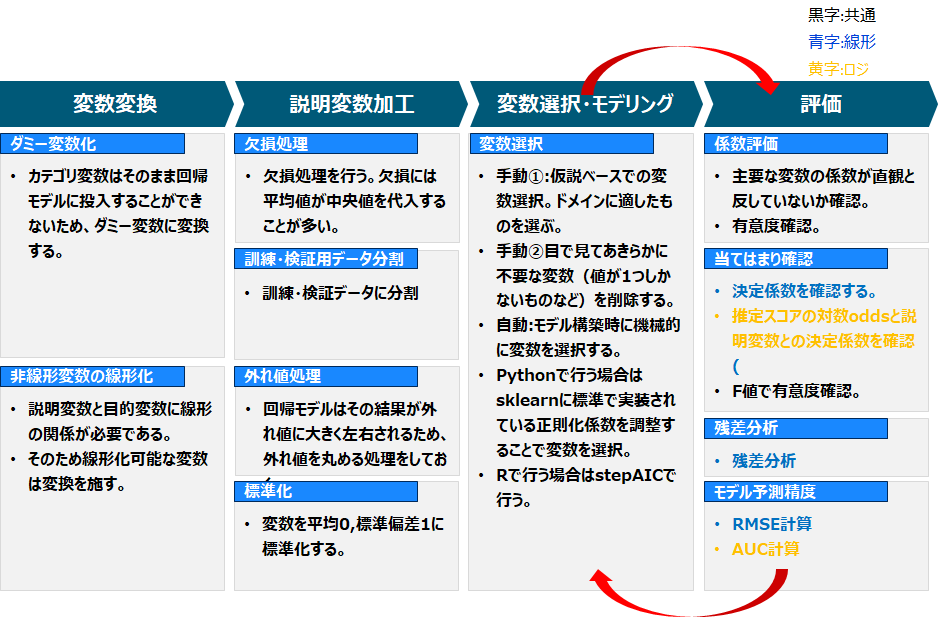
実習
実習用のpgmは以下のリンクからDLしてください
https://github.com/mitsu666/Lecture2021/blob/main/Lecture07_LogisticReg.ipynb
対象データ詳細
実験対象データは、UCI Machine Learning Repositoryより取得したCensus Income データセット「Adult Data Set」を用います。このデータセットには以下の変数が含まれており、この情報から年収が$50Kを超えるか否かを予測します。
age:年齢
workclass:雇用形態
fnlwgt:回答者への重み(メタデータ)
education:学歴
education-num:教育年数
marital-status:未婚・既婚ステータス
occupation:職業
relationship:続柄
race:人種
sex:性別
capital-gain:資本獲得
capital-loss:資本金の減少
hours-per-week:週あたりの労働時間
native-country:生まれた国
(参考) https://archive.ics.uci.edu/ml/datasets/adult
変数変換
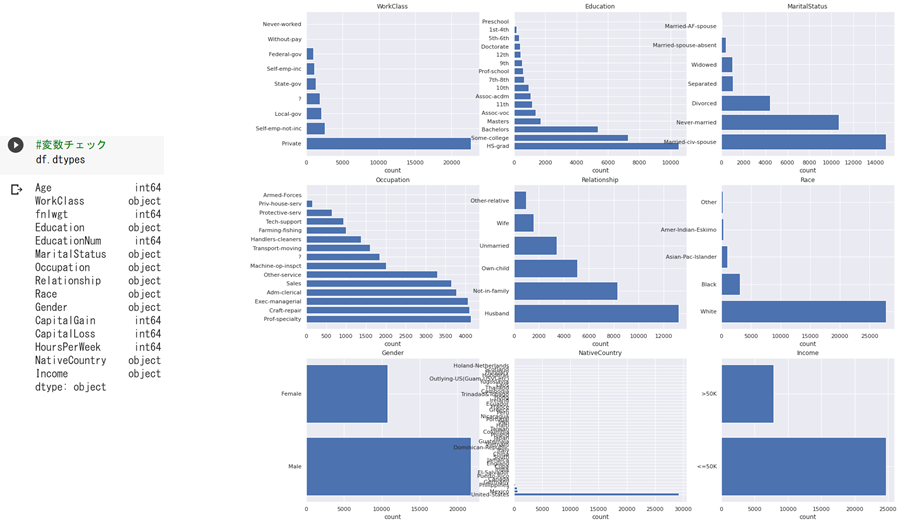
半分以上の変数がカテゴリタイプであるため変換が必要です。
目的変数を1/0に変換します。>50Kを予測するため、if >50K then 1 else 0と変換します。
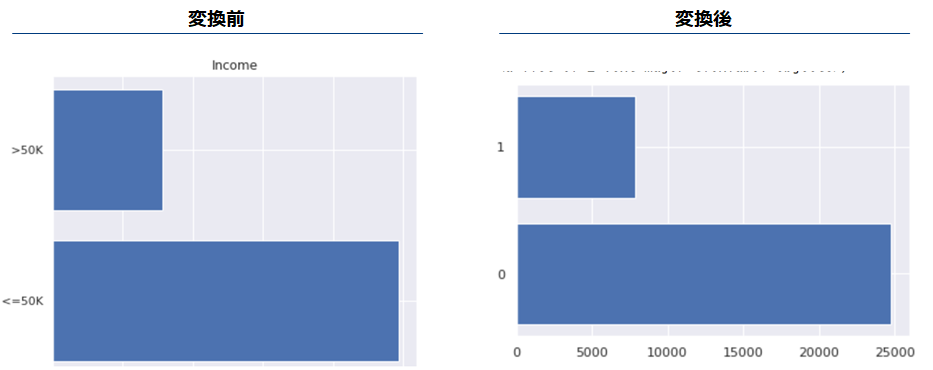
カテゴリ数が多い変数への対処します。カテゴリ数が多い変数(以下の赤囲みの変数)は、ダミー変数にする前に事前加工や変換が必要です。何故ならばそのままダミー変数にすると横に冗長なデータができるからです。
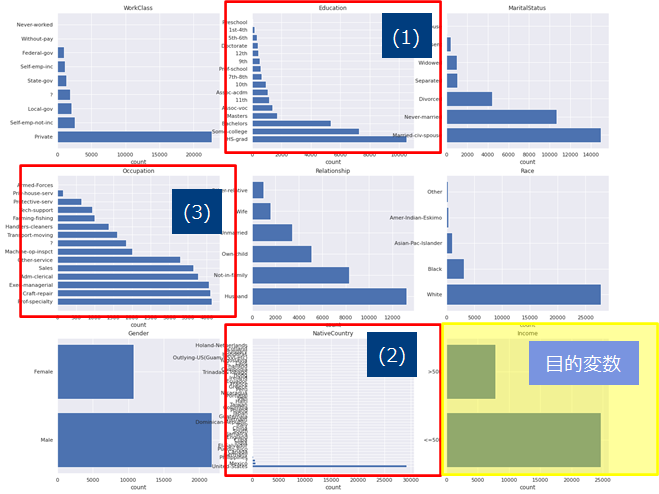
カテゴリ数が多い変数への対処(1) 順序変数
Educationは順序性を持つと考えられます(つまり、高学歴ほど高所得になりやすい傾向がある)従ってダミー変数化するのではなく、順序変数に変換します。
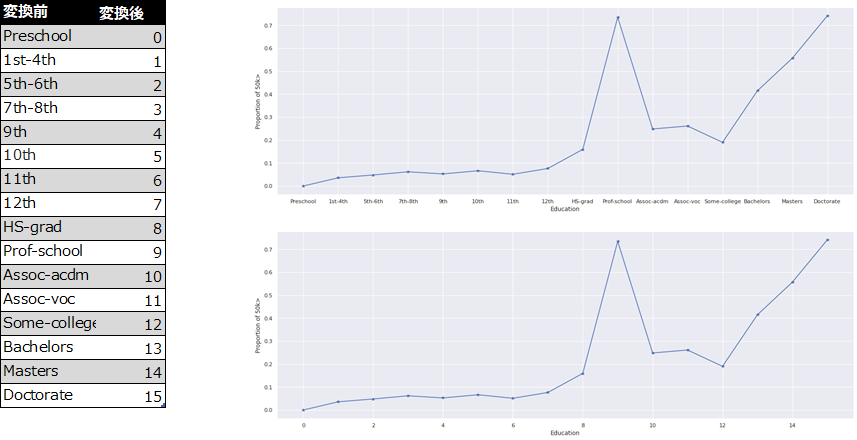
カテゴリ数が多い変数への対処(2) 多いものとそれ以外
「Native Country」の多くがアメリカであるため、アメリカかそれ以外の2値変数に変換します。
If Native Country ==アメリカ then 1 else 0という処理を行います。
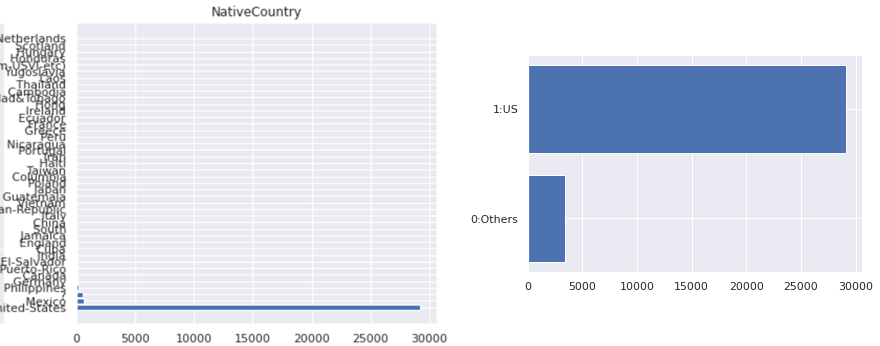
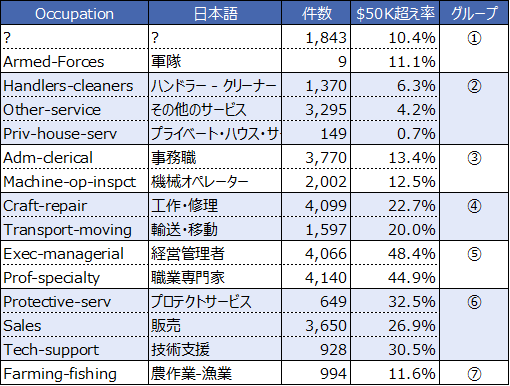
カテゴリ数が多い変数への対処(3) 似たグループでまとめる
ターゲット割合($50K超え率)が近しい値かどうか、社会通念上(またクライアントの知見上)類似した職業かどうかを基準にグループ分けをします。ターゲット割合が近い値であったとしても、「農作業-漁業」と「軍隊」のように職業特性が異なるものは同じグループにならないようにします。
残りのカテゴリ変数をダミー変数に変える
残りのカテゴリ変数「WorkClass」「MarialStatus」「Relationship」「Race」「Gender」をワン・ホット・エンコーディングします(ダミー変数化すると同義)。

特別処理
訓練(train)/検証(test)の分割を行います。この時点で 分けておきます。最善のタイミングは一番初めの作業の前です。しかし変数のダミー化などをする場合それぞれのデータセットで同じ処理を行うため、2度手間にならないようにそれらは分ける前のタイミングで行いました。以降の節からはtrainで学習した結果をtestに適用するためにこの時点でtrain/testに分けます。以下の図では5:5ですが、前回もやったように7:3とする場合が多いようです。
但しハイパーパラメータのチューニングを行う場合は、訓練の一部をバリデーションデータセットとして行います。(検証データを見ながらチューニングするのはNGです)
このブログ「」がとても詳しいので詳しく知りたい方はご参照ください。https://shirakonotempura.hatenablog.com/entry/2019/01/18/031645
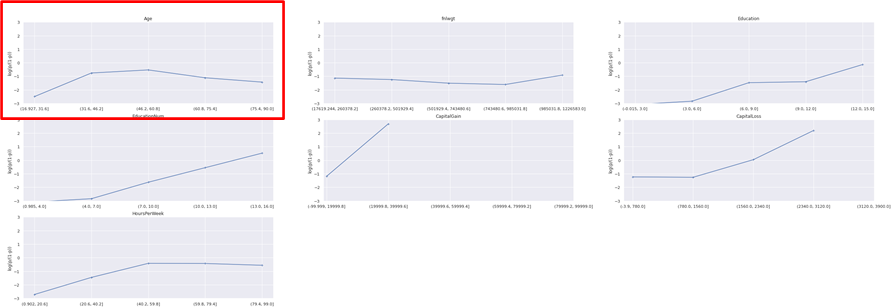
線形性チェック
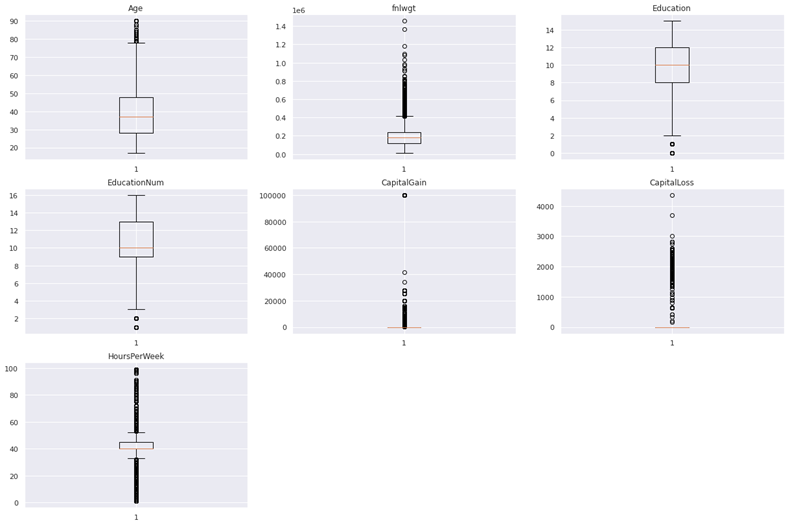
10以上のユニーク値を持つ数値変数とターゲット変数の対数oddsとの線形性をチェックします。
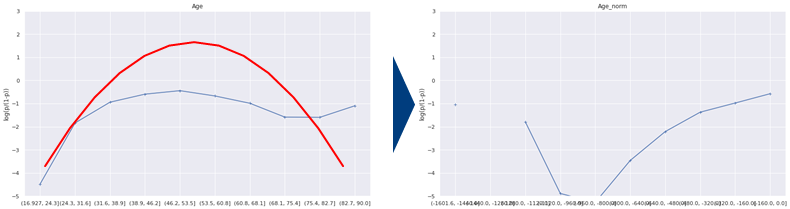
線形性のために変数変換
-1*(年齢-50)^2の変換を行う。つまり-x^2の変換をしています。一応両方の変数を取っておき、モデル精度の良い方を採用する方針としましょう。
説明変数加工
欠損確認
欠損なしです(まさかの)。
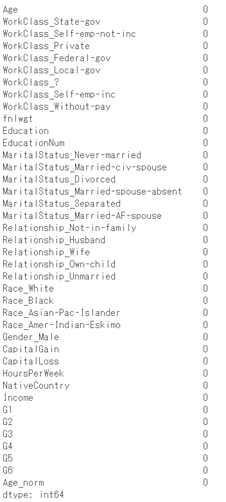
説明変数加工
標準化
標準化は 以下の手順ですが、テストデータを標準化する場合にも、x_mean及びx_stdは訓練データから算出したものを用います。(何故ならばテストデータは最後の評価まで使用できないからである。この段階でテストデータを使用してしまうと、モデルの一般的な性能の評価ができなくなる)

変数選択・モデリング
手動
線形回帰では散布図を描いて、目検及び相関係数の値(但しロジスティック回帰モデルでは相関係数の代わりにχ2乗統計量を参考にすること多い)を参考に採用変数を選択しました。しかし今回は変数が多いため、明らかに不要な「fnlwgt」というアンケートの重みづけというメタな変数をまず除きます。
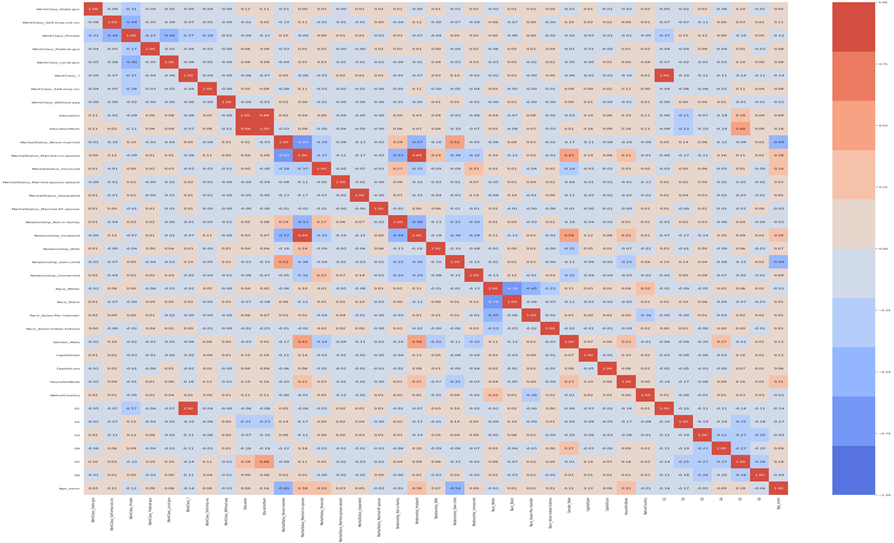
またAgeの変数変換後のAge_normとは相互どちらか削除(最初はAgeを削除)し、次に「EducationNum」と「Education」のように相関の強い変数を除きます。説明変数間の相関は相関係数を用いて判断します。今回は相関係数の絶対値が0.5を超えるペアの片方を削除します。
自動
変数増加法で変数を選択します、基準はAICが小さくなるようなモデルを選びます。pythonでは標準でこの機能を持つ関数がないため、自作した変数増加法の関数を使用します。 (pgmはjupyter notebook参照)
評価
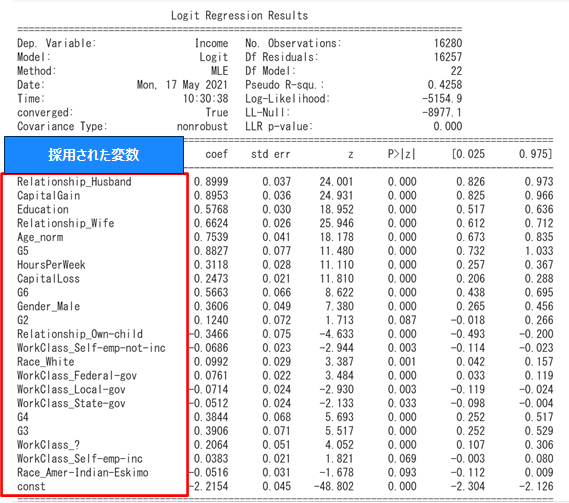
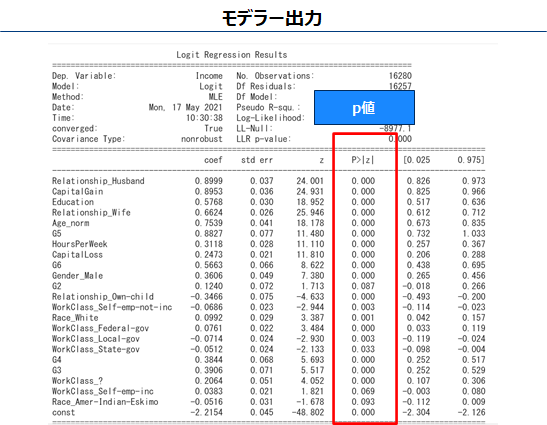
係数評価 解釈
選択された変数の係数の符号を確認します。符号が+(-)であれば当該変数が増加するほどターゲット割合、つまり$50K>の割合は増加(減少)します。
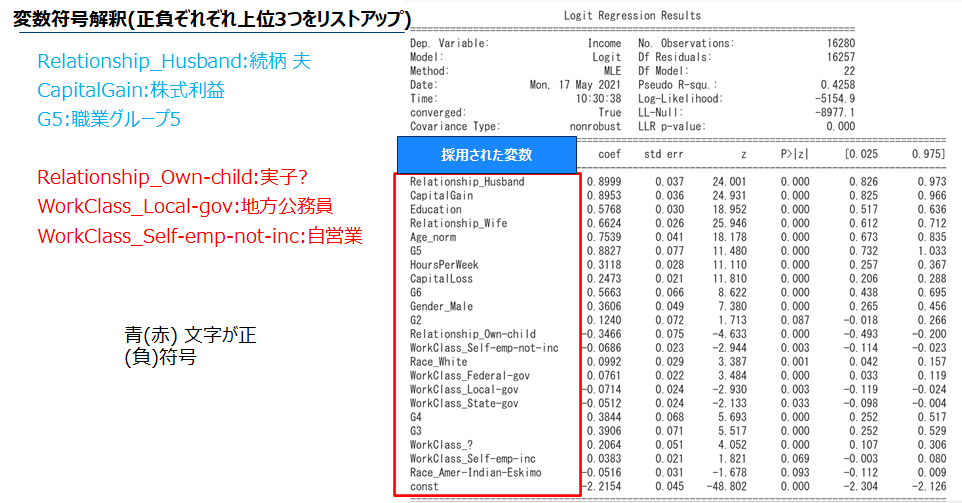
係数 有意検定
P値が十分小さければ変数の係数は有意(結果は偶然ではない可能性がある)、すなわち前項の解釈は正しそうと思ってよいです。(周りくどい言い回しになるのは、仮説検定自体が偶然たまたまそのようなデータが観測されたとは言い難いという消極的な対立仮説の採択をしているからである)1部の変数が5%基準で有意ではない。しかしこのまま解析を進めます。
補足
線形回帰の時に行った「モデル全体のあてはまりを評価するフェーズ」及び「残差分析」は行わいません。前者は、対応する指標として疑似決定係数や尤度比があるが直観的ではない事とモデル評価をROCやAUCで行う事が多いため予測モデルとして使用される場合省略されることが多いです。後者はそもそも誤差に正規性を仮定していないため不要です。
モデル予測精度 AUC
モデル評価指標としてAUCを用います。AUCは左下図ROCカーブの下の面積AUC(Area Under the Curve)である。識別力の高いモデルほど左上に膨れ上がり、その下の面積つまりAUCは大きくなります。AUCは0-1の値を取り、下図でBaselineとあるのがランダムモデル(つまりコインを振った表裏の結果により0/1と予測値を付与したモデル)であり、その精度は0.5です。これよりどれだけ大きいかでモデルの評価を行います。
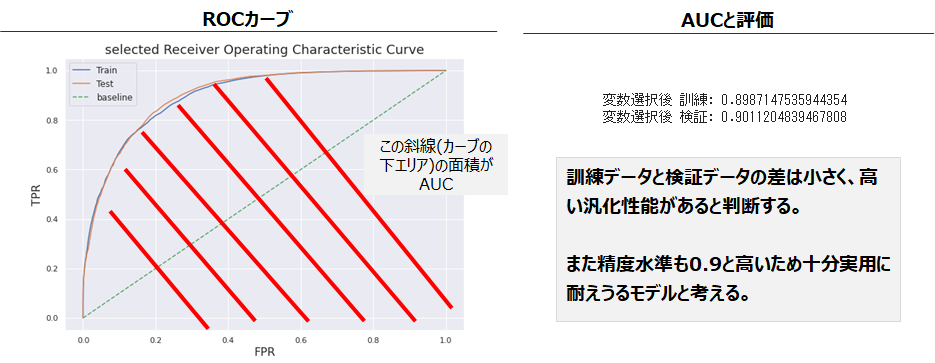
2値分類の評価指標として、正解率(Accuracy)、再現率(Recall)、適合率(Precision)などがあります。しかしそれぞれ問題設定によりみるべき指標が変わるため、実用的にはAUC及びROCカーブが用いられます。

