回帰モデルという言葉を恐らく、一度は耳にしたことはあるのではないかと思います。入力変数と目的変数の単純な相関関係を記述するモデルであり、そのために解釈が容易であること、Python/R/SAS/SPSSなど主要な言語やプラットフォーム全てで実行可能であることなどから非常に有効な手法として認知されています。
回帰モデルに書かれた書物は非常に沢山出版されていますが、一方でそれらを読んでも何となく分かったような分からないような気になった方も多いのではないのかと思います。これは理論に偏りすぎた説明をした本が多い、または実務的であっても「回帰モデル」というより「回帰分析」によった実務、例えば医療統計や社会学の統計など調査・研究向けに書かれた本が多いからではないかと推測します。
本稿ではマーケティングにおいてある値を予測したり、シミュレーションをしたりするために回帰モデルをどう使うかという観点から説明をしています。特にマーケティングで良く使用される、「線形回帰モデル」と「ロジステイック回帰モデル」を題材として取り上げ、その2つに共通する部分とそうでない部分ごとに、実務で活用するための急所をステップごとに解説します。リンクからpgmをダウンロードできるので、実際に手を動かしてそステップをご自身でなぞることで理解を深めることができます。
第1回は主だった一般論の解説と「線形回帰モデル」の説明をしていきます。
概要
回帰モデル 分類概要
数値及び質的変数を目的変数とする予測説明モデルの1種であり、教師あり学習に分類されます。主成分分析の時に用いた以下の分類では説明変数が数的変数の場合に限ると説明しましたが、実際は質的変数をダミー変数とすることで説明変数して扱うことが可能です。従ってここでは前者を狭義の定義とし、説明変数として質的変数も許容するものを広義の定義とします。(一般的には広義の意味で用いられることが多い)
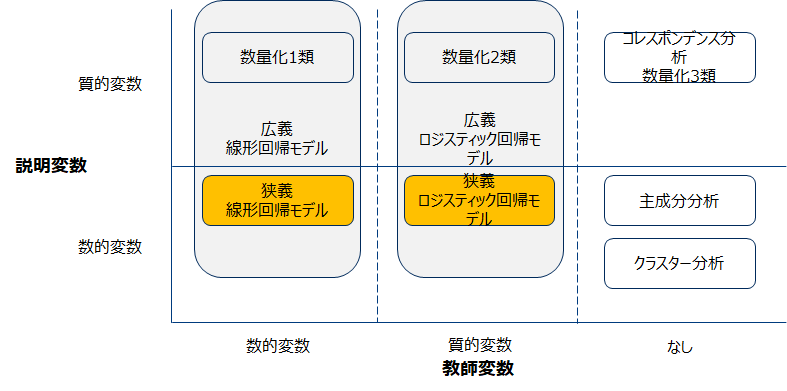
回帰モデル 一覧
回帰モデルは一般化線形化モデルといわれるモデル群のことを言います。このモデル群には線形回帰、ロジステイック回帰、ポアソン回帰などがあります。ここでは頻繁に用いる以下3つの概要に示します。これ以降は線形回帰モデルとロジスティック回帰に絞って話を進めます。何故ならばマーケティングの現場で用いる回帰モデルの8割程度はこの2つであるからです。

分析手順
分析手順 俯瞰図
線形回帰・ロジスティック回帰双方に共通しているプロセスを以下に示しました。
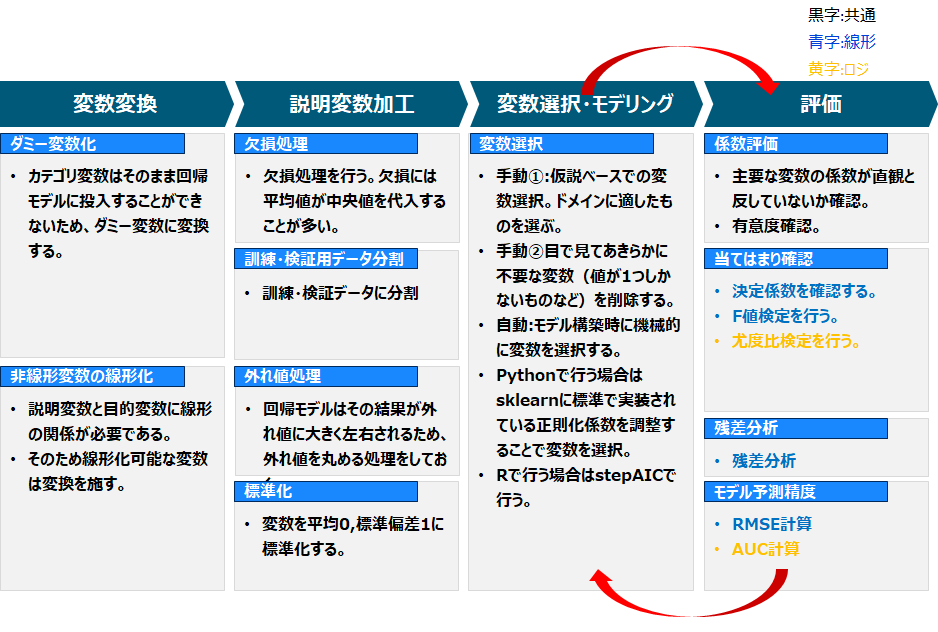
変数変換
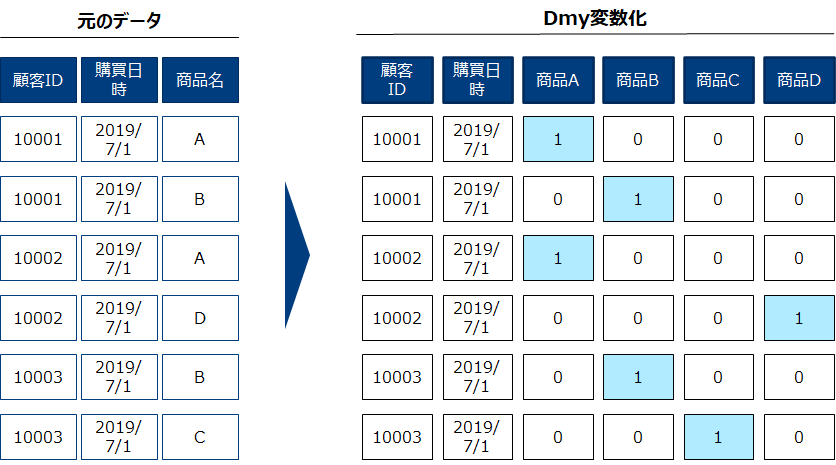
ダミー変数化
回帰モデルの投入するための適した形に変数を変換します。以下の「元のデータ」に内にある商品名のようなカテゴリ変数はそのままでは扱えないため、0/1の変数(ダミー変数)に変換しましょう。
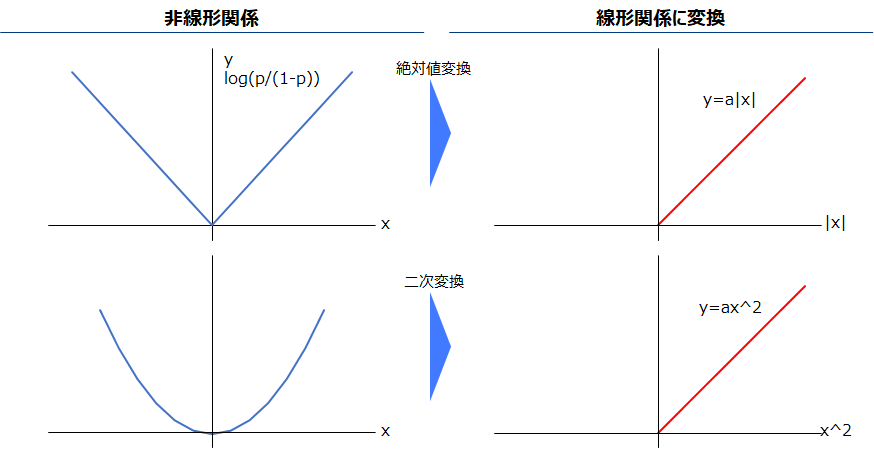
非線形変数線形化
線形回帰モデルは目的変数と説明変数の間に、線形(y=ax+bのような一次関数)の関係が必要であり、ロジスティック回帰はその目的変数の対数オッズ(log(p/1-p))と説明変数の間に線形関係が必要です。以下左のような目的変数と非線形関係がある場合、線形関係に変換します。
説明変数加工
欠損処理
欠損が説明変数にある場合、少数であればそのレコード自体を削除し、それ以外の場合欠損に何らかの値を代入します。何らかの値として平均値や中央値を用いる場合が多く、また小さい値や大きい値に寄せるためにmin,maxを代入する場合もあります。
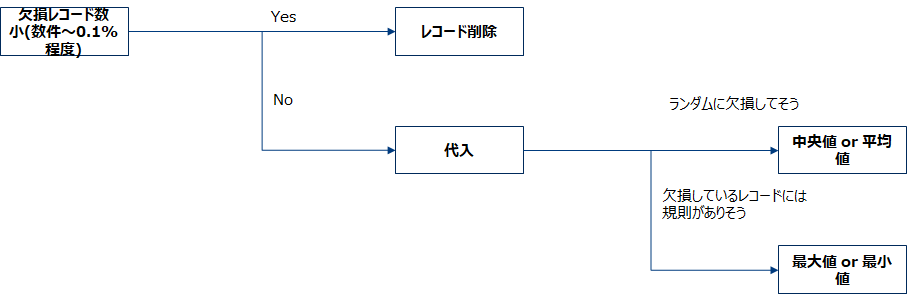
訓練・検証用データ分割
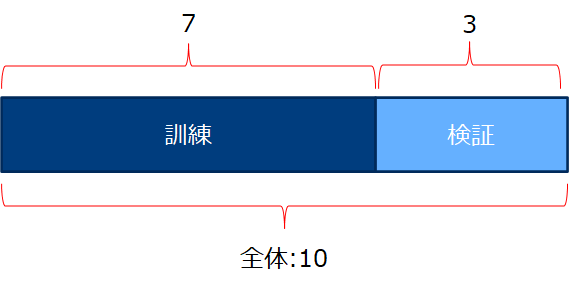
データを訓練用データセットと検証用データセットに分割します。この工程は外れ値処理や、標準化の前に行いましょう。何故ならば外れ値処理や標準化のパラメータを計算する場合に検証用のデータを含んだ形で計算してしまうと、検証データの情報が漏洩した状態になってしまうから適切な評価ができなくなります。分割方法はランダムに7:3で分けます。6:4でも構いませんがデータがとても多い場合(何百万件とある場合)は98:2のような分け方でも言いと最近は言われているようです。
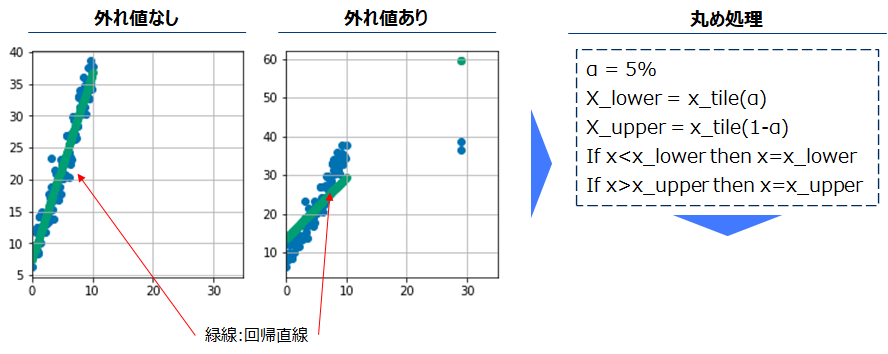
外れ値処理
下記左図のように、外れ値ありの場合回帰直線がその影響を受けます。そのために、外れ値を丸めることでこれを回避します。1-α%(α%)タイル点を外れ値に代入する方法で丸めることが多く、αは5,1などが適当です。訓練データの1-α%タイル点を用いて検証データにも同じ処理を行います。
標準化
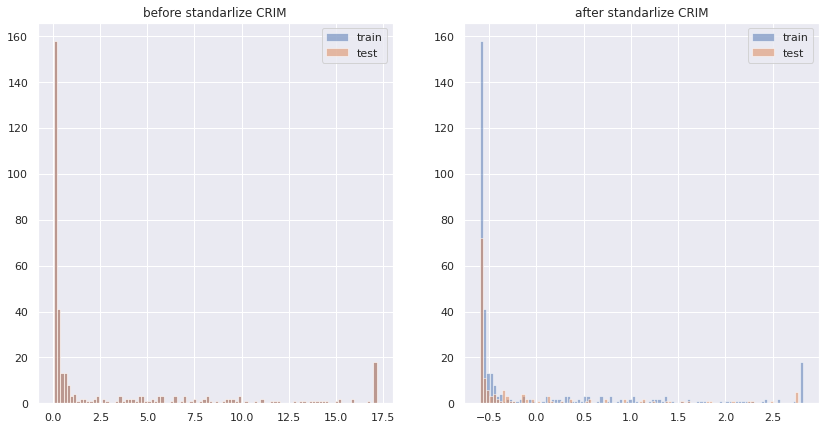
標準化の利点として、単位の異なる説明変数間同士で一次関数の係数の大きさを比較することができる、またロジスティック回帰に限っては勾配法の収束に良い影響を与えるなどがあります。訓練データの「平均値」と「標準偏差」を用いて検証データにも同様の処理を行います。

変数選択・モデリング
手動選択
モデルに投入する変数を選択します。その方法は分析者が手動で行う方法と、モデラーが自動で行う方法があり、一般的に手動で不要な変数を先に除いた後にモデラーに投入し、モデル構築をしながら変数選択を行います。手動で選択・削除する変数の基準例を以下にあげます。

モデリング 自動選択&モデリング
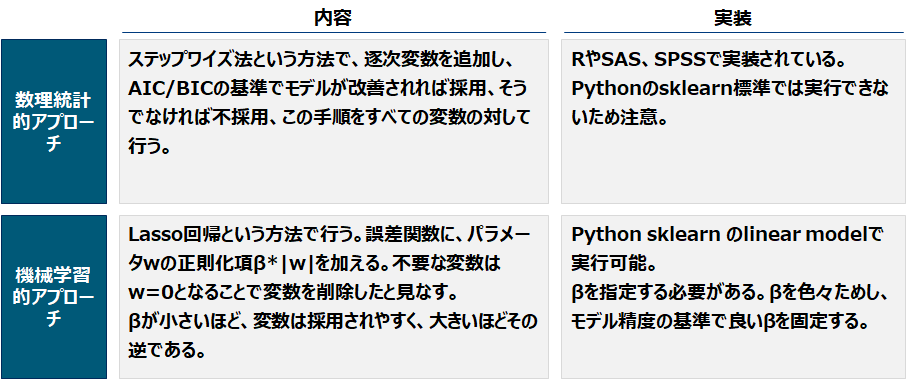
モデラーが自動で行う方法は数理統計的アプローチと、機械学習的アプローチがあります。前者は色々なパターンの変数の組み合わせを試し、その中で良い基準量を持つものを採用します。その基準量としてAICやBICのような情報量基準が用いられます。後者はlasso回帰と言われる手法でパラメータを採用した場合に誤差関数にペナルティを加えることで、モデル構築と変数選択を同時に行い、いずれもモデリングと同時に行います。
評価
出力 一覧
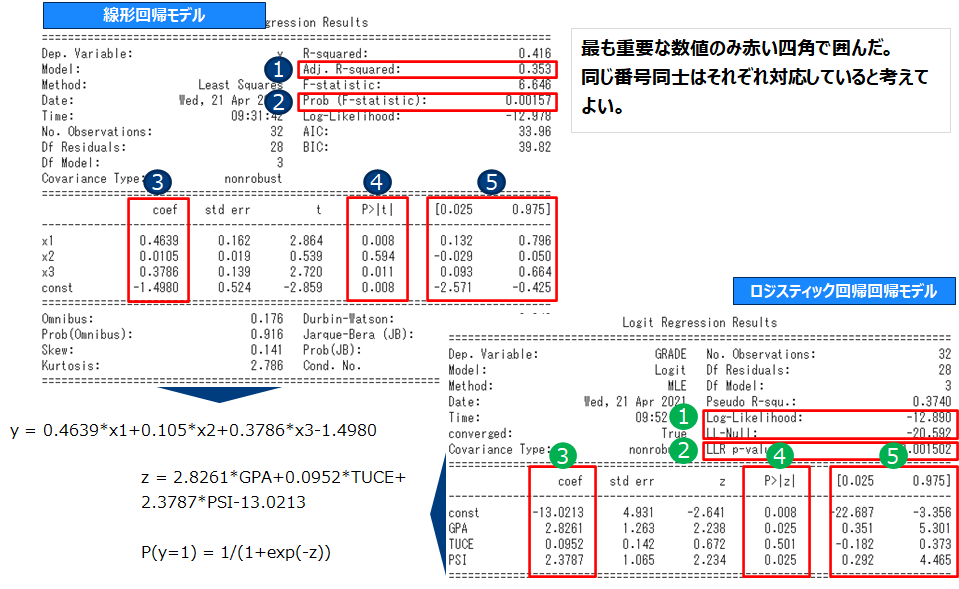
係数評価 & 当てはまり確認
上記の出力を以下の項目に対応させチェックしていきます。
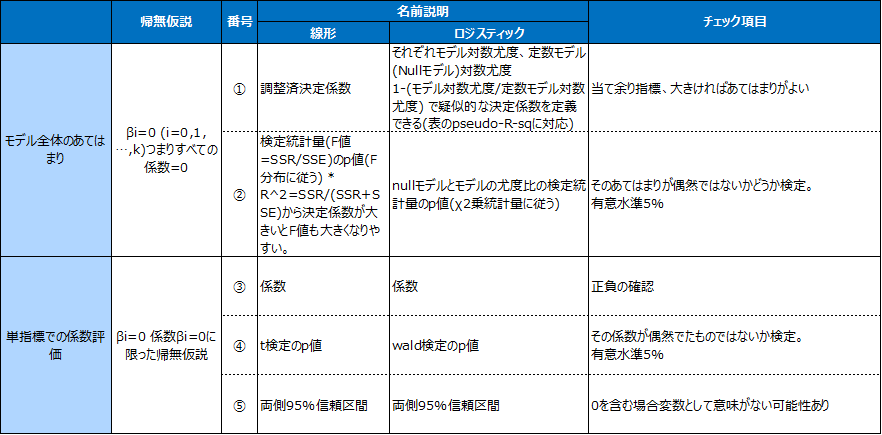
変数が一つだけの場合モデル全体のあてはまりの検証と単指標での係数評価はほぼ同じことをしているため、片方だけで良いです。
(参考) その他補足
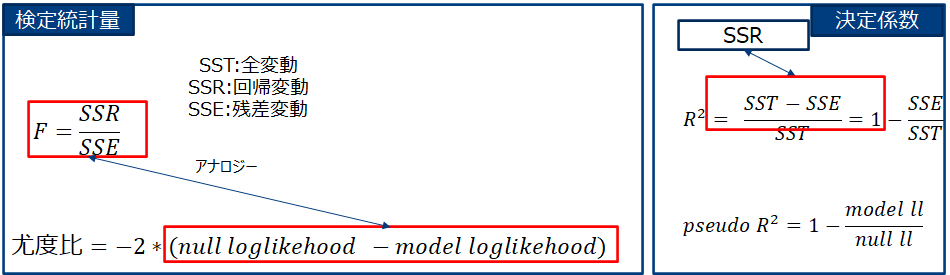
決定係数は変数の数を大きくしていくと、どこまでも大きくなるため、変数の数でペナルティを与え調整する。これが調整済決定係数です。調整済決定係数:=1 – 回帰誤差/(レコード数-パラメータ数) ÷ 全体分散 / (レコード数-1) よりnが大きい場合は調整済決定係数≒決定係数です。(ロジスティック回帰モデルの場合は疑似(pseudo)決定係数がある)。
線形回帰ではβi=0 (i=1,..,n)という仮説をSSEとSSRの比(正確には自由度で各々を除した数の比)つまりSSR/SSEを統計量として検定しており。他方ロジスティック回帰では同様の仮説を尤度比 -2*(nullモデル対数尤度 – モデル対数尤度)を統計量として検定しています。
実習 線形回帰モデル
以下からは冒頭のgithubのリンク先にあるpgmを実行しながら確認して進めていくようにしてください(記事内にpgmはありません)。
対象データ詳細
実験対象データは、sklearnに付属しているbostonというボストンの住宅価格のデータセットを用います。各カラム名は以下の通りです。
CRIM: 町別の「犯罪率」
ZN: 25,000平方フィートを超える区画に分類される住宅地の割合=「広い家の割合」
INDUS: 町別の「非小売業の割合」
CHAS: チャールズ川のダミー変数(区画が川に接している場合は1、そうでない場合は0)=「川の隣か」
NOX: 「NOx濃度(0.1ppm単位)」=一酸化窒素濃度(parts per 10 million単位)。この項目を目的変数とする場合もある
RM: 1戸当たりの「平均部屋数」
AGE: 1940年より前に建てられた持ち家の割合=「古い家の割合」
DIS: 5つあるボストン雇用センターまでの加重距離=「主要施設への距離」
RAD: 「主要高速道路へのアクセス性」の指数
TAX: 10,000ドル当たりの「固定資産税率」
PTRATIO: 町別の「生徒と先生の比率」
B: 「1000(Bk – 0.63)」の二乗値。Bk=「町ごとの黒人の割合」を指す
LSTAT: 「低所得者人口の割合」
MEDV:「住宅価格」(1000ドル単位)の中央値。通常はこの数値が目的変数として使われる
(引用元) https://www.atmarkit.co.jp/ait/articles/2006/24/news033.html
変数変換
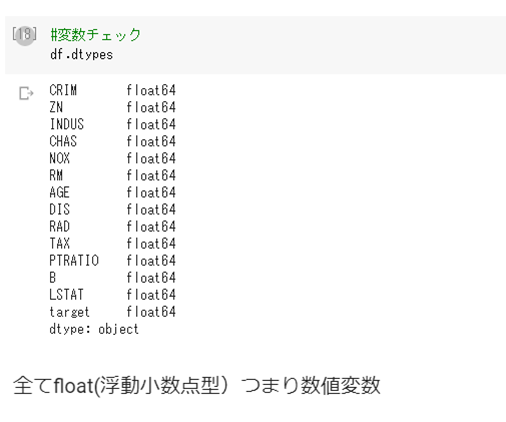
変数タイプ確認
全て数値変数であるためダミー変数にする必要はないようです。
線形性確認
線形性を確認します、以下を見る通りどの変数も問題ないです。
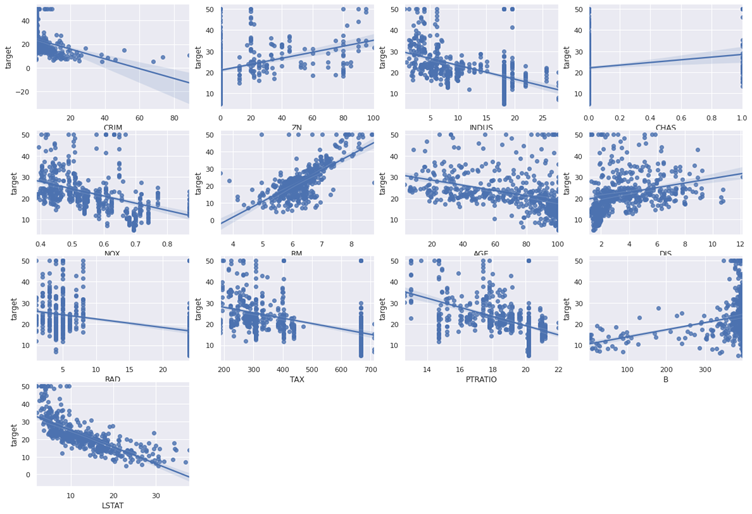
説明変数加工
欠損確認
さすがのトイ・データだけあって欠損はありません。
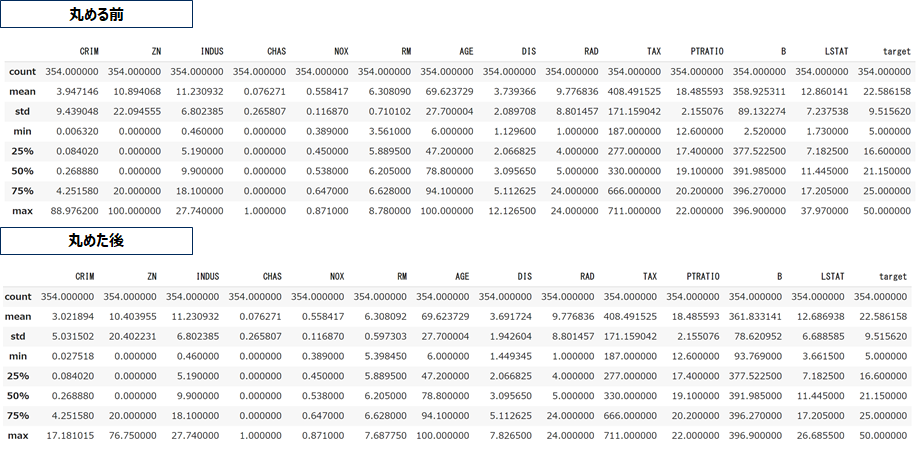
外れ値処理
5%/95%タイルで丸めました。(この数値に理論的な根拠はない、慣習的に99%や95%で丸めることが多い)
標準化
変数選択・モデリング
手動
右下散布図と左下表にあるtargetとの相関係数から不要な変数を削除します。ここではすべての変数がtarget(つまり住宅価格)に対して説明力を持っていそうですので、このまま削除せずに進めていきます。
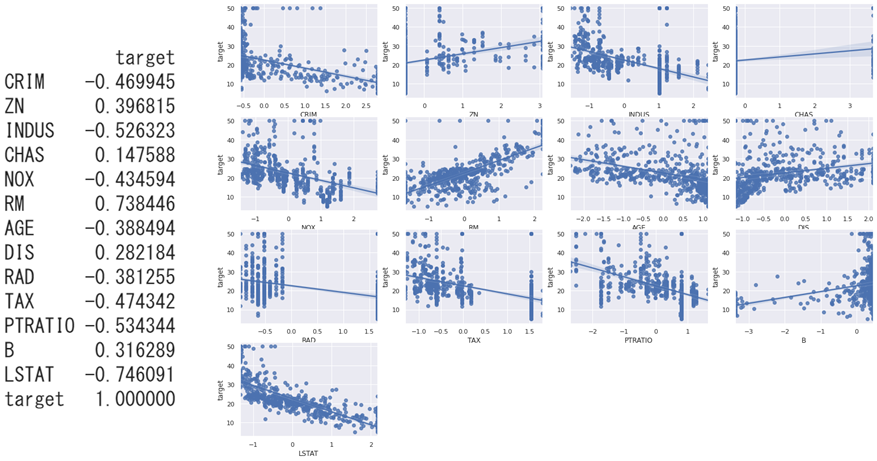
自動
変数増加法で変数を選択します、AICが小さくなるようなモデルを選びます。pythonでは標準でこの機能を持つ関数がないため、自作した変数増加法の関数を使用します。 (pgmはjupyter notebook参照)
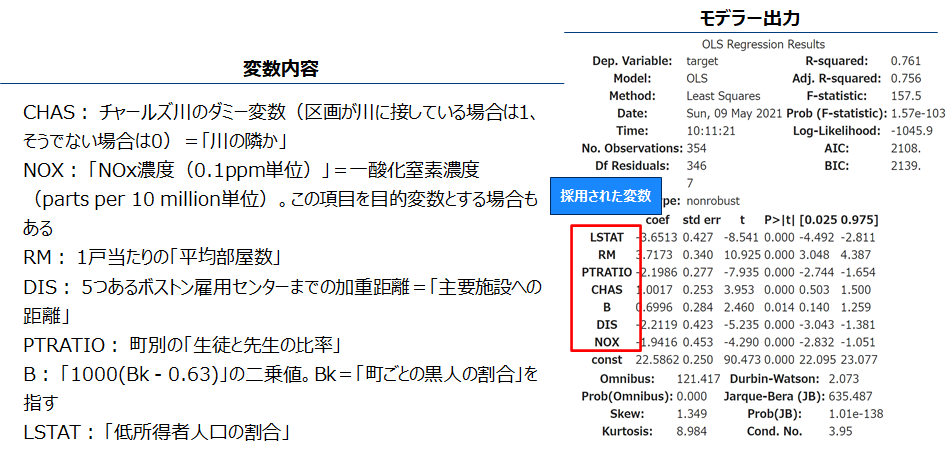
評価
係数評価 解釈
選択された変数の係数の符号を確認しましょう。符号が+(-)であれば当該変数が増加するほどターゲット変数(住宅価格)は向上(低下)します。
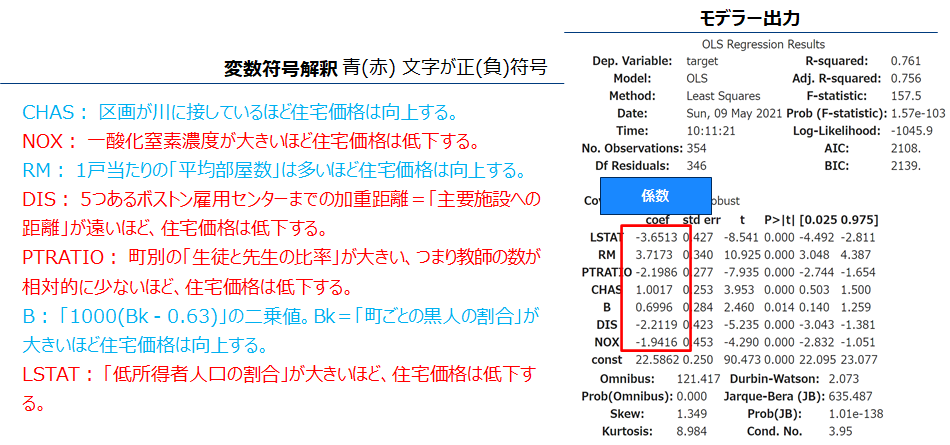
係数評価 有意度検定
P値が十分小さければ変数の係数は有意(結果は偶然ではない可能性がある)、すなわち前項の解釈は正しそうと思ってよいです(周りくどい言い回しになるのは、仮説検定自体が偶然たまたまそのようなデータが観測されたとは言い難いという消極的な対立仮説の採択をしているからである)。全ての変数でp値<0.05であるため5%水準で有意であるといえます。
余談ですがp値は使用が難しい手法で、うっかりするとすぐ間違った使い方をしていることがあります。そのためあまりこういうところで触れたくないのですが、この話をしている以上は避けては通れないというジレンマがあります。データが多いとほんの僅かな差でさえ有意となってしまうこともあり、ビッグデータの時代には不要なものとなるかもしれません。
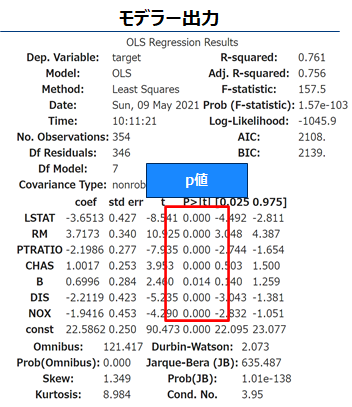
当てはまり確認
モデル全体の当てはまりを確認しましょう。調整済決定係数(0<=R2<=1)は0.756で全変動の7割以上を回帰モデルで説明できているようです。さらにF値のp値<1.57e-103<0.05でありモデル全体としても5%水準で有意です。
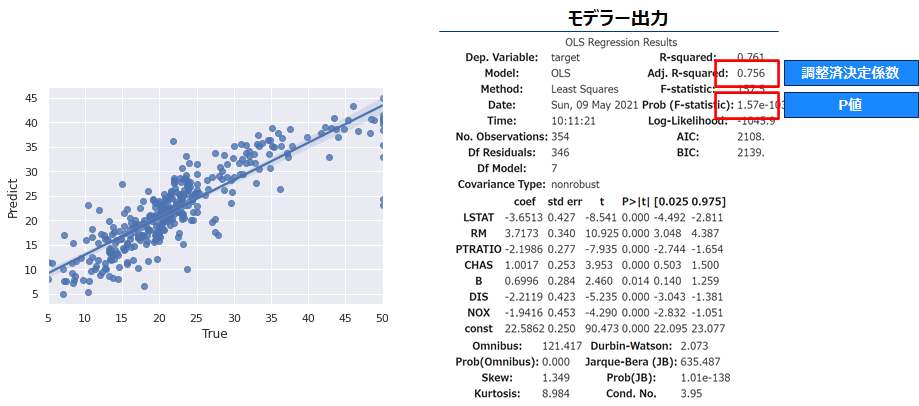
残差分析
線形回帰モデル(not ロジスティック回帰モデル)は誤差に以下を仮定しています。
- 誤差は正規分布に従う。
- 誤差分散は均一である、つまり目的変数の値によらずその誤差のばらつきは同程度である。
- 誤差同士は無相関
これらの仮定に誤差がちゃんと従っているかを確認します。QQプロットは対角線(黄色の線)上にのっていればその誤差は正規分布に従っていると考えられます。残差プロットはその赤いラインのx座標によらずどの場所でも赤いラインを中心に均等にばらついているかを確認します。
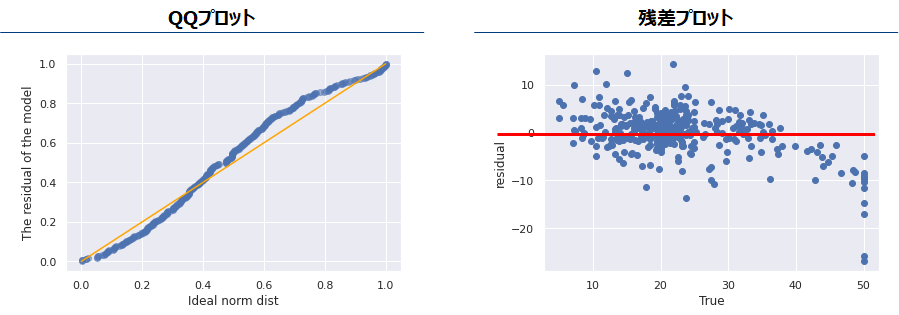
残差プロットでは一部正解変数の値が大きい箇所で極端に誤差が大きくなる箇所があります。これはこの回帰モデルの説明変数では説明できないような要因があることを示しています。しかし他に追加できるデータがないため、今回はこのまま続けます。
モデル予測精度
訓練データと検証データそれぞれでRMSEを計算します。2つの差が小さいとき、モデルは汎化性能を持つと考えてよいということになります。しかしこの差が大きい場合、特に構築データのRMSEが検証データのそれより低い場合、モデルがデータに過剰に適合している可能性があるため、投入変数を減らすデータを増やすなどして対応します。
最後に
おそらく、本内容は専門家の方がみたら突っ込みたくなる箇所が多いかもしれません。しかしマーケターの現場ではとにかくやってみようという精神が重要であるのも事実です。そのため本記事は極力難しい検定や汎化誤差に関しての議論は簡易かつベターと思われる方法で記述し、とにかくデータから回帰モデルを1本作るということができるようになることを主眼としています。
次回はロジステイック回帰を説明します。

